|
4.2 Построение матриц жесткости конечного элемента Общий порядок построения матрицы жесткости последним на примере конечного элемента пластины, показанного на рис. 4.3, а, б . Толщину пластины обозначим ?. Необходимо составить выражение потенциальной энергии деформации U, выразив его через вектор обобщенных узловых перемещений 
Из п. 3.1 имеем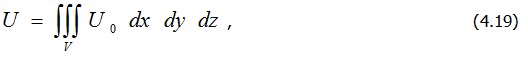 
где плотность энергии деформации для плоского напряженного состояния будет 
Здесь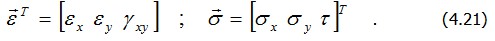 
Используя формулы Коши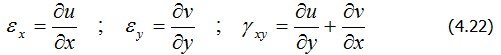 
и выражение для поля перемещений в элементе (4.12), найдем 
В кратком виде эти равенства запишем так: 
где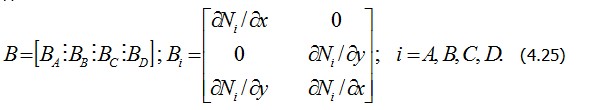 
Закон Гука в обратной форме для плоского напряженного состояния дает соотношение 
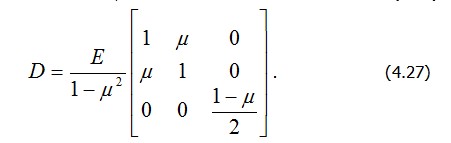
Следовательно, 
Учитывая, что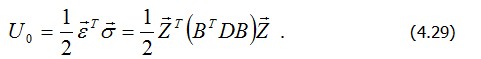 
Подставив (4.29) в (4.19), приведем выражение для энергии деформаций элемента к виду 
Перепишем (4.9), заменив старое обозначение обобщенных перемещений 
Сравнивая (4.29) и (4.30), можем записать общее выражение для матрицы жесткости, отвечающей вектору перемещений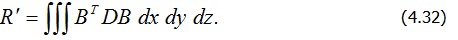 
Штрих у R подчеркивает, что матрица жесткости получена в местной системе координат, связанной с элементами. Штрихи у x и y в этом параграфе опущены.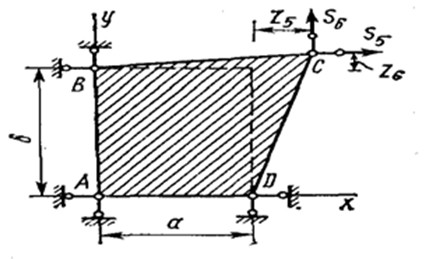 
Рис. 4.6 Для пластины толщиной 
где А – площадь элемента Интегрирование в этих формулах ведется поэлементно. Число элементов матрицы зависит от числа обобщенных перемещений 
Матрица В, переводящая вектор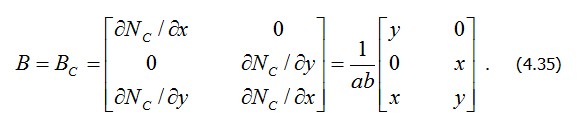 
Подставив (4.35) и (4.27) в (4.33), получим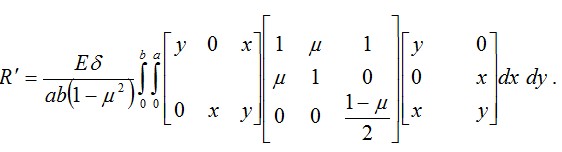 
После перемножения трех матриц под знаком интеграла придем к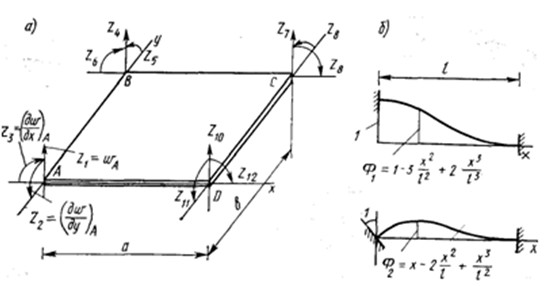 
Рис. (4.7) симметричной матрице размера 2*2, интегрируя каждый элемент которой в указанных пределах окончательно найдем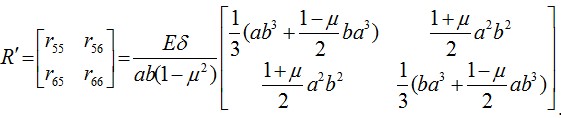 
Формула (4.33) носит общий характер, хотя и получена на примере плоской задачи. Чтобы ею воспользоваться, необходимо построить только две матрицы, а именно: матрицу закона Гука D , связывающую напряжения и деформации (или усилия и деформации), и матрицу В, которая позволяет перейти от перемещений к деформациям в элементе. Это иллюстрируется далее на примере задачи изгиба пластины. Рассмотрим прямоугольный конечный элемент изгибаемой пластины (рис. 4.7, а). В каждом узле примем за неизвестные три обобщенных перемещения: прогиб , два угла поворота нормали и . Следовательно, полный вектор обобщенных перемещений элемента состоит из 12 компонент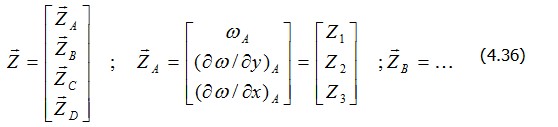 
и элемент имеет 12 степеней свободы. Выражение поверхности прогибов элемента зададим так, чтобы оно содержало 12 постоянных коэффициентов, например в виде следующего полинома: 
Выражая параметры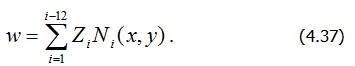 
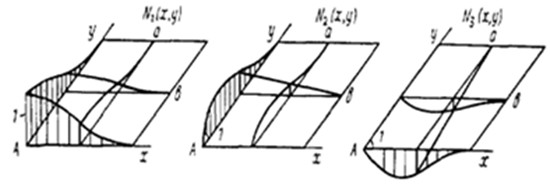
Рис. (4.8) Так, для узла А первые три базисные функции будут: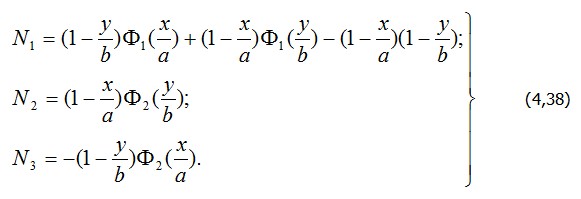 
где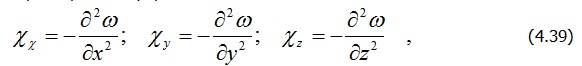 
которым отвечают изгибающие и крутящие моменты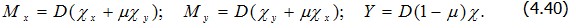 
Энергия деформации элемента пластины создается за счет деформаций (4.40), связанных с законом Гука 
где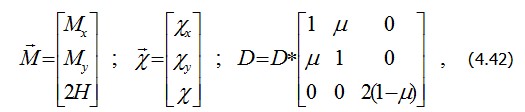 
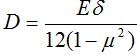
- цилиндрическая жесткость пластины. Матрицу B, связывающую деформации 
где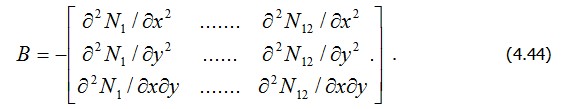 
Подставляя D и В в формулу (4.33) и заменив в ней интегрирование по объему интегрированием по площади пластины, получим формулу для вычисления матрицы жесткости конечного элемента при изгибе: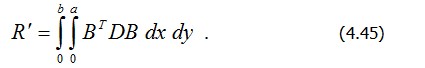 
|
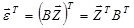одставив (4.28) и (4.24) в (4.20), получим
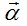на
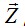используемое в МКЭ: 
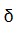интеграл
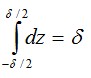и вместо (4.32) можем написать 
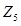и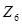 
для элемента, показанного на рис. 4.6. Вектор 
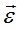по (4.24), состоит из одного блока 
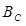что с учетом (4.11) дает 
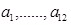через
перейдем к базисным функциям (функциям нормы)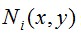
: 
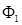и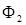 
- функции, выражающие линию прогибов защемленной по концам балки от единичного смещения или угла поворота заделки (рис. 4.7, в). Вид трех базисных функций
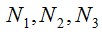изображен на рис. 4.8. Остальные функции
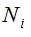в (4.37) строятся аналогично.
Известно, что каждый элемент пластины испытывает три характерные деформации: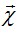 
и перемещения 
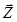элемента, получим, подставляя (4.37) в (4.39):