

|
4.3 Общая процедура расчета по МКЭ Проследим основные этапы использования МКЭ на конкретном примере расчета плоской конструкции, изображенной на рис. 4.9, а. На первом этапе выбирается расчетная схема и наносится сетка конечных элементов. На рис. 4.9, б показана рассматриваемая половина конструкции ввиду ее симметрии с выбранной сеткой квадратных элементов а = b = 20 см. Там же дана нумерация узлов и конечных элементов (в кружках). От нумерации узлов зависит структура матрицы системы уравнений, к которой сводится решение задачи. Матрица имеет ленточную структуру, схематически показанную на рис. 4.9, б.
В заштрихованной ленте шириной 2М в каждой строке могут находиться ненулевые элементы, вне ее все элементы нулевые. Это связано с тем, что, в уравнения равновесия узла входят лишь обобщенные силы, соответствующие элементам, примыкающим к этому узлу. Можно сказать, что данный узел непосредственно «взаимодействует» только с ближайшими окружающими его узлами.
При нумерации надо стремиться к тому, чтобы наибольшая разность номеров «взаимодействующих» узлов была как можно меньше. В данном случае общее число неизвестных перемещений за вычетом перемещений закрепленных на границе узлов будет n = 2*133-2*7-7=245. Таков порядок системы уравнений в данной задаче; полуширина ленты М=30. ленточность структуры уравнений является большим достоинством МКЭ, так как упрощает и ускоряет решение уравнений.
На следующем этапе строятся матрицы жесткости отдельных элементов в местной системе координат 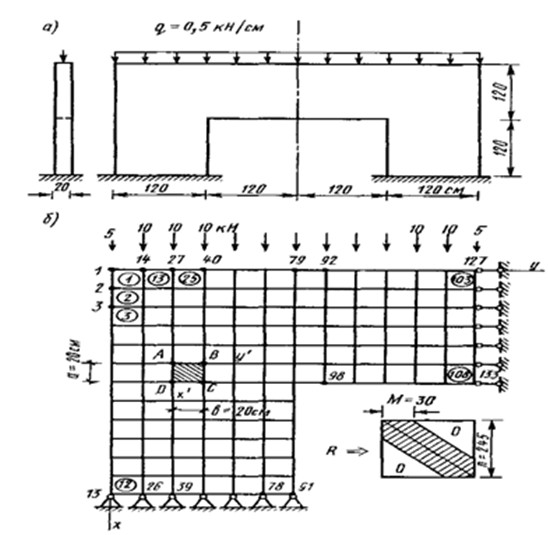
Рис. (4.9) Наконец, после того как найдены перемещения узлов каждого элемента 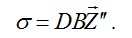
На рис.4.10 показана общая картина перемещений узлов (с увеличением в 500 раз), а на рис. 4.11 – эпюры напряжений в двух сечениях конструкции. В расчетах принято 
Рис. (4.10) 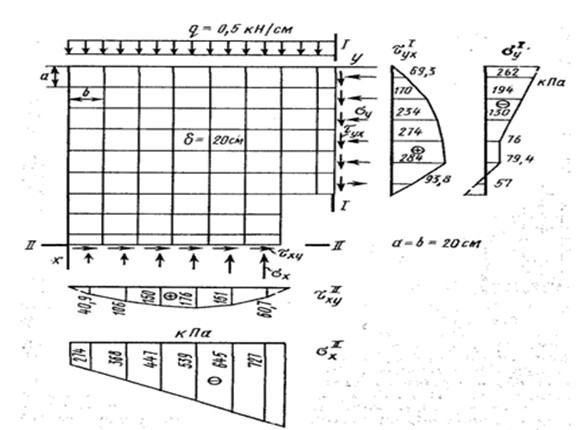
Рис. (4.11) Это только основы МКЭ. |

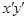 В данном случае все элементы одинаковые и матрицы
В данном случае все элементы одинаковые и матрицы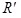 строились, как описано в § 8.9. В общем случае они могут быть различными по форме, материалу, размерам.
Далее из матрицы
строились, как описано в § 8.9. В общем случае они могут быть различными по форме, материалу, размерам.
Далее из матрицы 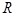 в общей системе координат
в общей системе координат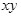 В данном случае неизвестные в местной системе
В данном случае неизвестные в местной системе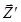 и в общей системе
и в общей системе 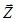 по направлению совпадают. Они лишь имеют различную нумерацию. Так, показанный на рис. 4.9, б 30-й элемент ABCD в соответствии с рис. 4.3, а, б будет иметь нумерацию неизвестных:
по направлению совпадают. Они лишь имеют различную нумерацию. Так, показанный на рис. 4.9, б 30-й элемент ABCD в соответствии с рис. 4.3, а, б будет иметь нумерацию неизвестных:
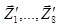 . В то же время в общей системе в узлах A, B, C, D номера неизвестных будут
. В то же время в общей системе в узлах A, B, C, D номера неизвестных будут 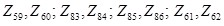 Поэтому элементы должны будут попасть в соответствующие клетки общей матрицы жесткости .
Такая рассылка элементов матриц жесткости отдельных конечных элементов с их суммированием в клетках общей матрицы
Поэтому элементы должны будут попасть в соответствующие клетки общей матрицы жесткости .
Такая рассылка элементов матриц жесткости отдельных конечных элементов с их суммированием в клетках общей матрицы 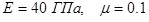 В заключение отметим, что здесь изложены лишь начальные основы МКЭ. Более подробные сведения можно найти в учебнике [2] и в специальной литературе.
В заключение отметим, что здесь изложены лишь начальные основы МКЭ. Более подробные сведения можно найти в учебнике [2] и в специальной литературе.