

|
4.1 Сущность метода конечных элементов Метод конечных элементов (МКЭ) является методом приближенного прямого отыскания неизвестных функций на основе какого-либо вариационного принципа. Зародившись в строительной механике, он получил широкое распространение в решении различных проблем математической физики – в задачах теплопроводности, гидро и аэродинамики, фильтрации и других задачах физики. Здесь мы ограничимся знакомством с этим методом с позиции, наиболее близких к строительной механике. Он имеет достаточно широкую математическую трактовку. За три десятилетия существования и развития этого метода наиболее развитой оказалась та его разновидность, когда решение ведется в перемещениях. Она связана с вариационным принципом Лагранжа и может быть истолкована как усовершенствованная модификация метода Ритца. Рассмотрим эти вопросы на примере решения плоской задачи для пластины, нагруженной в ее плоскости (рис. 4.1, а). 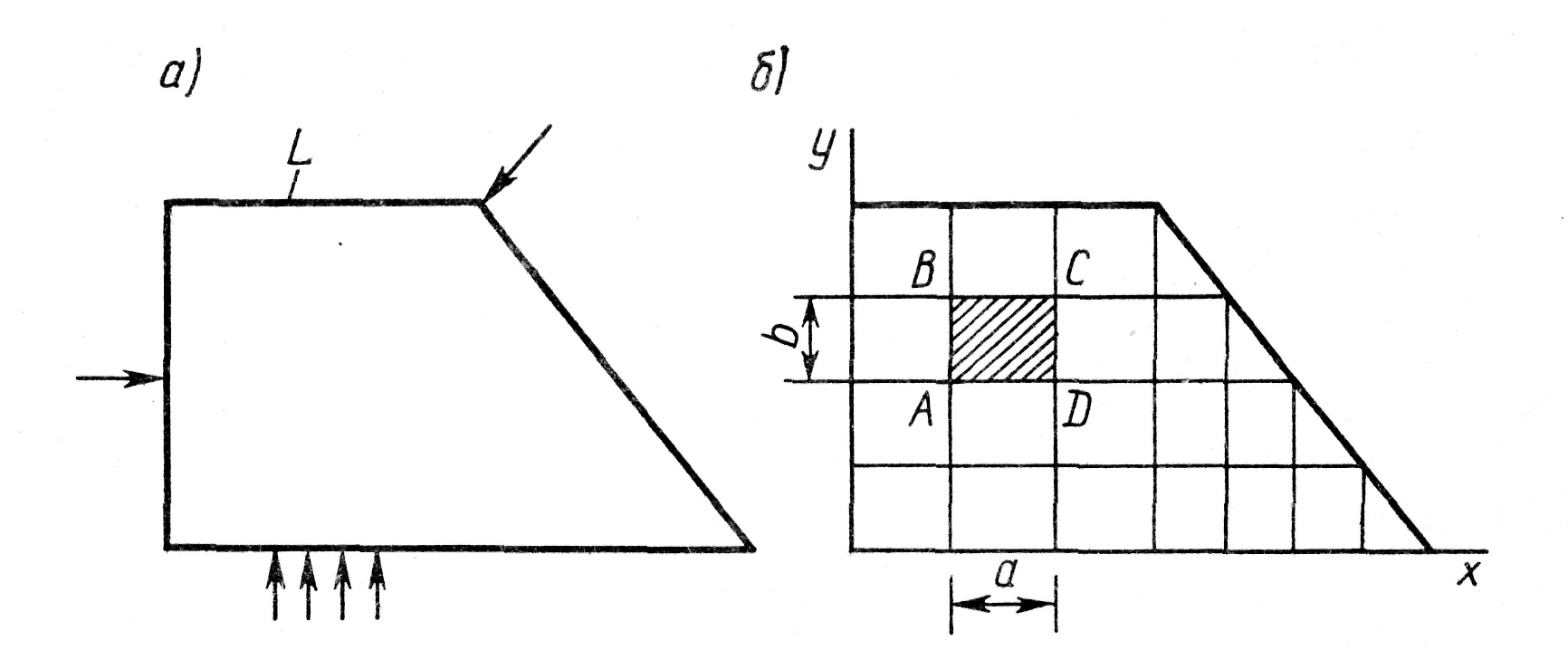
Согласно методу Ритца, перемещение u и v задаются в виде сумм 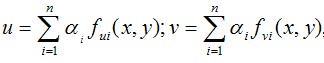 (4.1) где – обобщенные перемещения (числа), подлежащие определению; В § 3.5 показано, что (4.2) выражающих условия равновесия в виде равенства нулю суммарной обобщенной силы, отвечающей каждому обобщенному перемещению 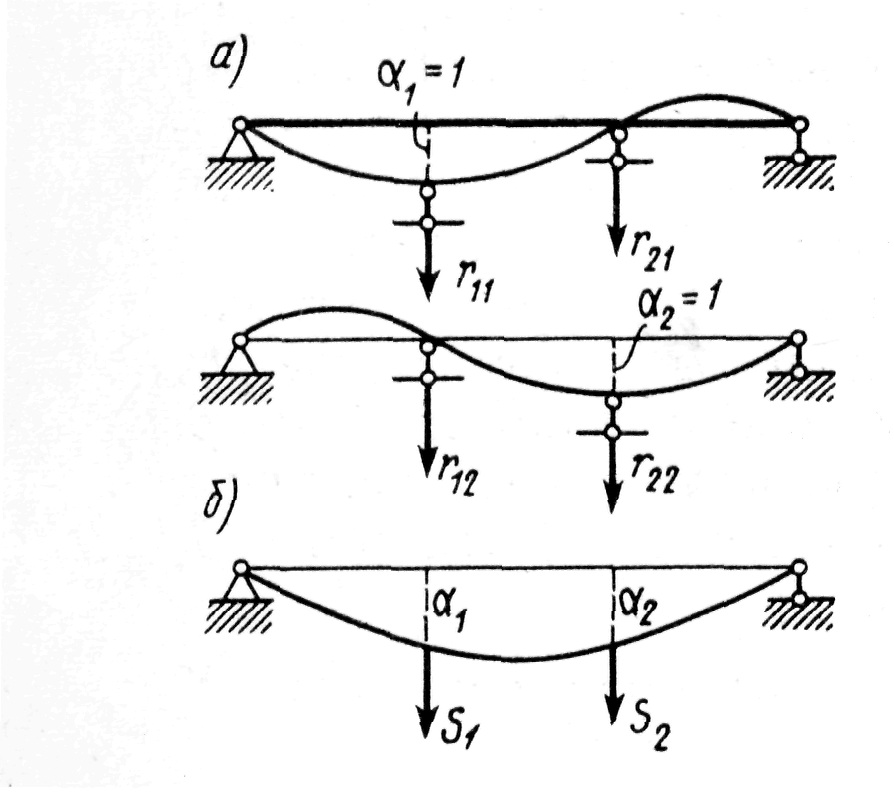
В линейно-деформируемой системе вектор обобщенных сил упругости 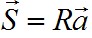
где 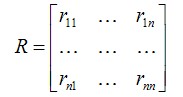 называется матрицей жесткости, отвечающей вектору обобщенных перемещений 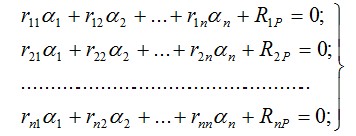 (4.5) Или в матричной записи 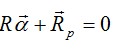
Из решения этих уравнений и определятся искомые обобщенные перемещения Остановимся подробнее на понятиях матрицы жесткости R и обобщенной упругой силы 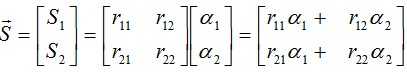
Подчеркнем, что понятие обобщенной силы имеет энергетическую природу и в общем случае величина Si не обязательно представляет собой реальную силу, как это имело место в рассмотренной балке. Из формулы 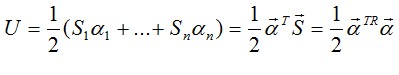
Развернув это равенство, можно видеть, что оно представляет матричную запись квадратичной формы 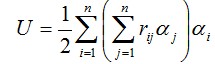
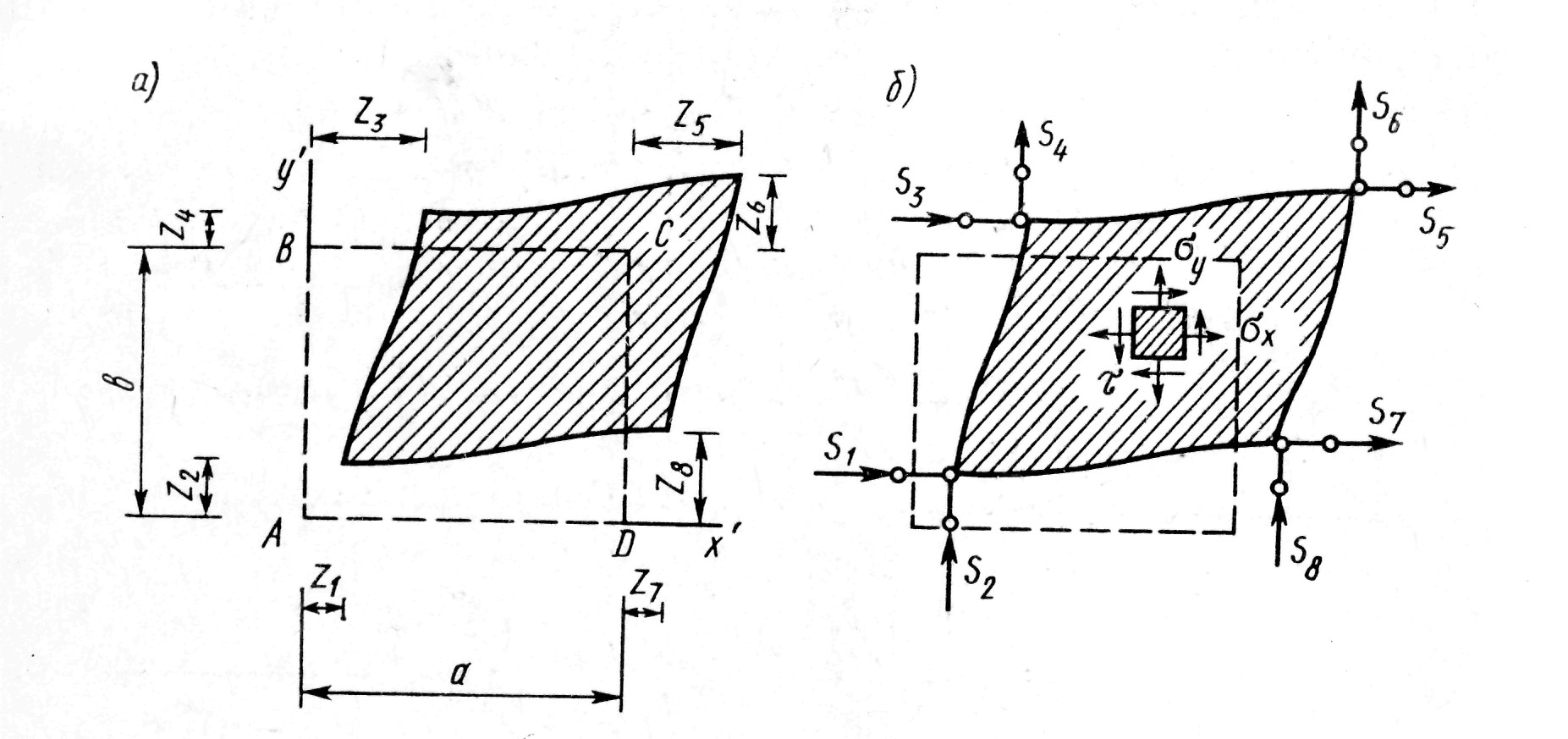
которой в (3.27) выражалась энергия деформации U. Выражение (4.9) используется в дальнейшем при получении общей формулы, служащей построения матрицы жесткости R, роль которой очень важна, так как именно с ее помощью образуются разрешающие уравнения (4.5). Трудность применения метода Ритца в описанном виде состоит в том, что для тела сложной формы, в том числе и рассматриваемой пластине, очень сложно, практически невозможно, подобрать такую систему базисных функций в равенствах (4.1), которая будучи заданной на всём поле пластины с контуром L (см. рис. 4.1, а), позволяла бы учесть различные местные особенности ее напряженно-деформированного состояния. Метод конечных элементов (МКЭ) устраняет эту главную трудность. Разобьем пластину сеткой на отдельные элементы конечных размеров, как это для примера показано на рис. 4.1, б. Поле перемещений u и v будем задавать отдельно в пределах каждого конечного элемента. В качестве обобщенных перемещений прием перемещения узловых точек элемента, которые принято вместо обозначать Zi. На рис. 4.3, a показаны восемь таких перемещений, полностью определяющих деформированное состояние некоторого элемента ABCD. Поле перемещений элемента выразим через узловые перемещения в системе координат x’y’, связанной с элементом (местной системе координат) 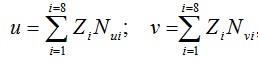
где Nui=Nui (x’, y’) и N vi = N vi (x’, y’) - базисные функции, заданные в пределах элемента. Их строят так, чтобы в соответствующих узловых точках они имели значение, равное единице, а в остальных узлах обращались в ноль. В (4.10) множители Zi приобретают смысл как бы амплитудного значения для соответствующего слагаемого. Например, введем такие четыре функции (рис. 4.4): 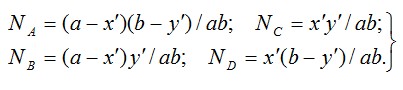
Тогда выражения (4.10) могут быть записаны в соответствии с указанным свойством базисных функций так: 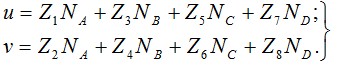
При таком задании перемещений энергия деформации рассматриваемого элемента будет полностью определяться его узловыми перемещениями Z1, . . . , Z8. Поэтому, аналогично (4.3), для него можем написать соотношение между обобщенными силами упругости и перемещениями: 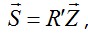 (4.13) где 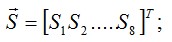
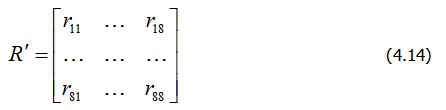
выше, равна работе внутренних сил упругости элемента при любых деформированных состояниях, определяемых перемещениями 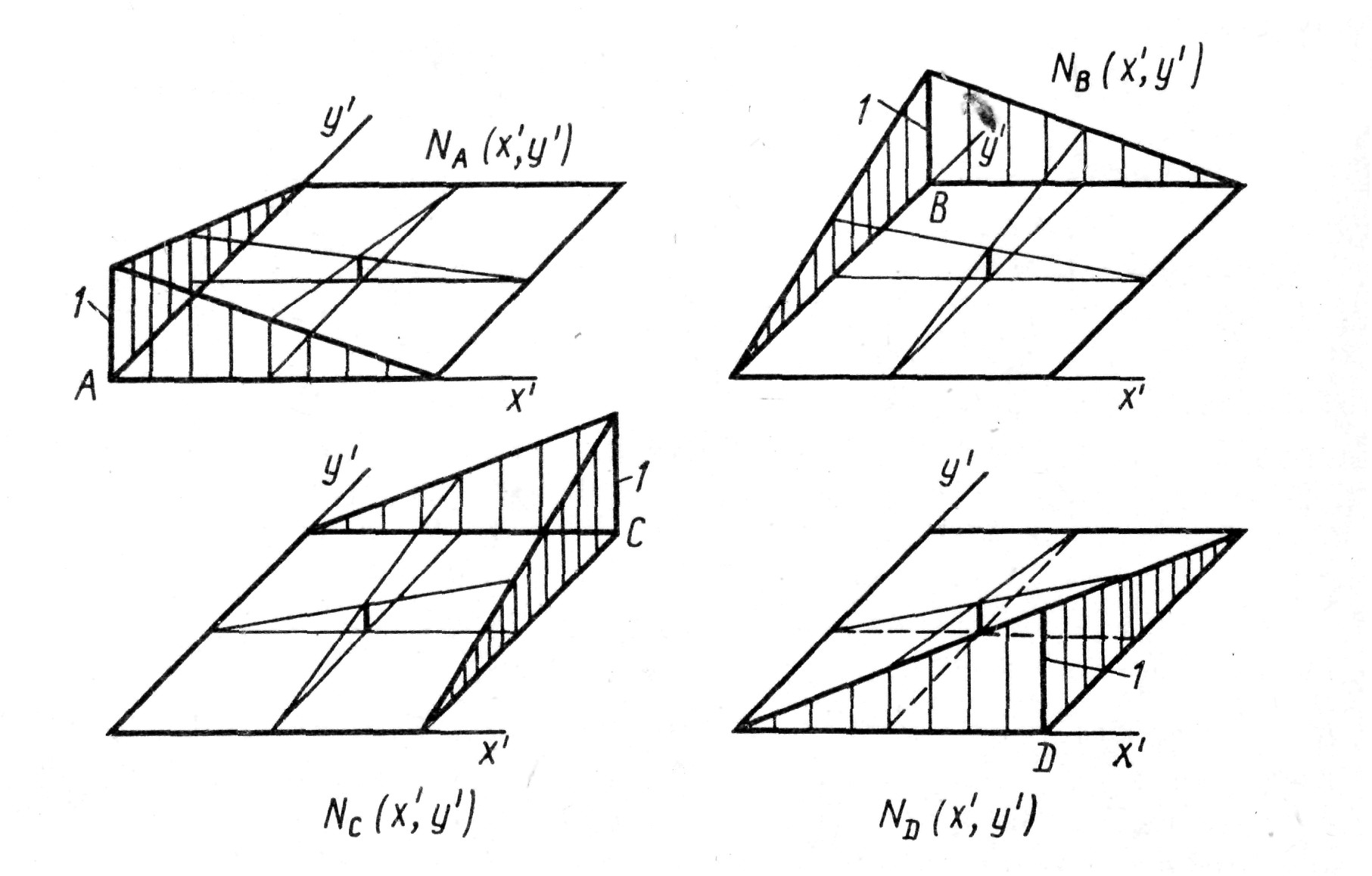
Рис. 4.4 В узловые точки элемента введены связи, которым сообщили перемещения Z1 , . . . ,Z8,, возникшие в связях реакции S1 , . . . ,S8 , уравновешивающие (в смысле равенства работ) упругие силы деформированного элемента, и есть то, что находится с помощью матрицы жесткости R? и соотношения (4.13). Заметим, что тоже относится и к грузовому слагаемому в (4.2): - это реакция в i-й связи от внешней силы, приложенной в данном узле.Рассмотрим теперь отдельный узел сетки конечных элементов, у которого перемещения будут Z k и Z k+1 (рис. 4. 5). Он окружен четырьмя элементами: I, II, III, IV. Условие равновесия k-го узла, согласно методу Ритца (4.2), запишется как равенство нулю суммарных обобщенных сил по k-му и (k+1)-му направлениям: 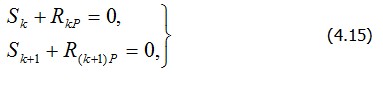
где 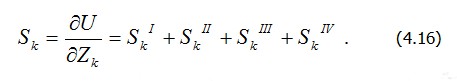
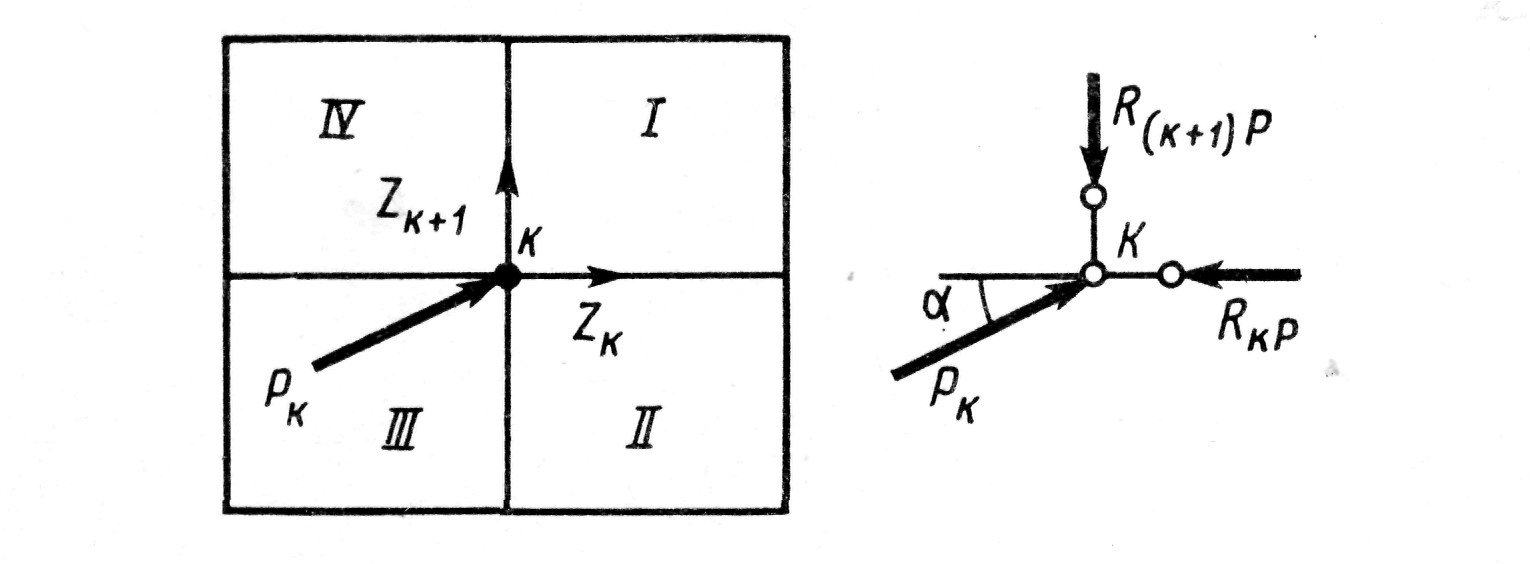
Рис. 4.5 Аналогичное выражение будет и для Sk+1 . Оно показывает, что в уравнениях равновесия типа (4.15) войдут обобщенные упругие силы только от примыкающих к узлу конечных элементов. Это следует из механической модели обобщенных упругих сил, изображенной на рис. 4.3, б. Формально это можно доказать тем, что энергия деформации пластины равна сумме энергий отдельных элементов: 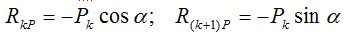
В результате уравнения, выражающие равновесие всех узлов конечно-элементной системы, получат вид 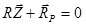
Рис. (4.17) где 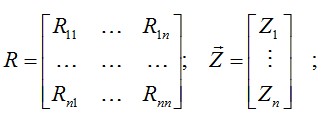
n – общее число неизвестных обобщенных перемещений в конструкции; R – матрица жесткости ансамбля конечных элементов, образующих заданную конструкцию. Каждый элемент ее строится, как это следует из изложенного, путем соответствующего суммирования элементов матриц жесткости, примыкающих к узлу конечных элементов. |

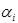
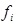 –базисные функции, которыми задаемся в пределах площади пластины.
–базисные функции, которыми задаемся в пределах площади пластины.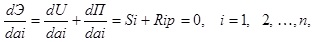
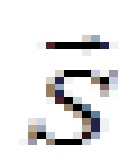 выражается через обобщенные перемещения
выражается через обобщенные перемещения 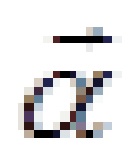 с помощью матрицы R:
с помощью матрицы R: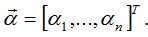 .В развернутой форме уравнения (4.2) имеют вид
.В развернутой форме уравнения (4.2) имеют вид 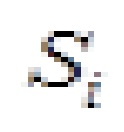 . На рисунке 4.2, a элементы матрицы проиллюстрированы на примере балки, в которой в качестве обобщенных перемещений приняты прогибы
. На рисунке 4.2, a элементы матрицы проиллюстрированы на примере балки, в которой в качестве обобщенных перемещений приняты прогибы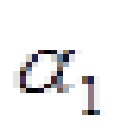 и
и 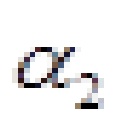 . Силы
. Силы 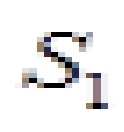 и
и 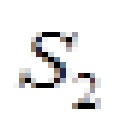 связаны с ними соотношением (рис. 4.2, б)
связаны с ними соотношением (рис. 4.2, б)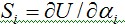 следует, что
следует, что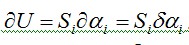 Это равенство говорит лишь о том, что произведение Si на малое приращение должно быть равно изменению энергии деформации системы, численно равной работе всех сил упругости на деформациях системы, отвечающих перемещения . Следовательно, в общем случае, Si может рассматриваться как некоторый условный силовой фактор, связанный с обобщенным перемещением указанным соотношением. В зависимости от вида перемещения величина Si может быть истолкована как сила, момент и т. д. Энергия деформации системы U как работа обобщенных сил на
перемещениях будет
Это равенство говорит лишь о том, что произведение Si на малое приращение должно быть равно изменению энергии деформации системы, численно равной работе всех сил упругости на деформациях системы, отвечающих перемещения . Следовательно, в общем случае, Si может рассматриваться как некоторый условный силовой фактор, связанный с обобщенным перемещением указанным соотношением. В зависимости от вида перемещения величина Si может быть истолкована как сила, момент и т. д. Энергия деформации системы U как работа обобщенных сил на
перемещениях будет
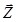 Следовательно, в данном случае обобщенные силы получают наглядное истолкование – их можно представить как сосредоточенные силы в узлах элемента так, чтобы они совершали работу на соответствующих узловых перемещениях Z (см. рис. 4.3, б).
Здесь необходимо сделать одно замечание. Из теоретической механики известно, что обобщенная сила равна производной от энергии по обобщенному перемещению с обратным знаком. В уравнениях Ритца (4.2) знак минус опущен и упругой силой названа сама производная акую силу надо рассматривать как силу, противоположно направленную силам упругости, т. е. уравновешивающую эти силы. Механически можно представить себе это так, как изображено на рис.
4.3 б).
Следовательно, в данном случае обобщенные силы получают наглядное истолкование – их можно представить как сосредоточенные силы в узлах элемента так, чтобы они совершали работу на соответствующих узловых перемещениях Z (см. рис. 4.3, б).
Здесь необходимо сделать одно замечание. Из теоретической механики известно, что обобщенная сила равна производной от энергии по обобщенному перемещению с обратным знаком. В уравнениях Ритца (4.2) знак минус опущен и упругой силой названа сама производная акую силу надо рассматривать как силу, противоположно направленную силам упругости, т. е. уравновешивающую эти силы. Механически можно представить себе это так, как изображено на рис.
4.3 б).