

|
3.7 Температурные напряжения Пусть во всем объеме тела, свободного от закреплений, температура изменяется на одинаковую величину T . Это приводит к всестороннему увеличению (уменьшению) линейных размеров тела. При этом относительная величина линейной температурной деформации равна Если изменение температуры неравномерно по объему или тело имеет соответствующие закрепления, то свободное температурное расширение одних частей тела будет стеснено взаимодействием с другими частями. В результате в теле появляются дополнительные температурные напряжения. Из курса сопротивления материалов известны приемы определения температурных напряжений в простейших статически неопределимых стержневых системах. Здесь покажем определение таких напряжений в более общих случаях. Формально изменение температуры тела T вносит лишь изменение в запись закона Гука из числа основных уравнений теории упругости. Так, для плоского напряженного состояния он получит вид: в прямой форме 
в обратной форме 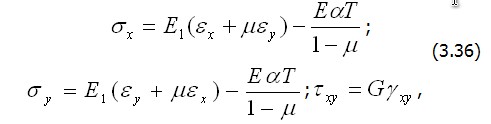
где Все остальные уравнения теории упругости остаются без изменения. Поэтому температурная задача может решаться как обычная задача упругости, но с измененной записью закона Гука. Практически для того, чтобы можно было воспользоваться соответствующими готовыми разрешающими уравнениями (в напряжениях или в перемещениях), удобно бывает свести указанную температурную задачу к задаче о действии на тело некоторой дополнительной нагрузки. Рассуждаем при этом следующим образом. Пусть тело получило изменение температуры 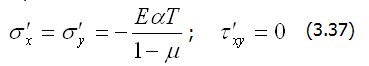
Для того чтобы эти напряжения могли существовать в теле в общем случае, к нему должна быть приложена некоторая нагрузка. Из уравнений равновесия (2.3) найдем необходимую нагрузку: 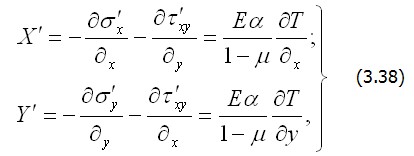
А из уравнений равновесия на поверхности тела 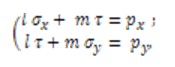
соответствующую поверхностную нагрузку: 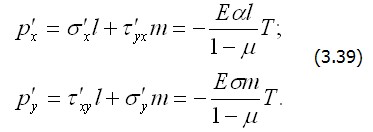
Итак, при одновременном изменении температуры T (x,y) и приложении объемной (3.38) и поверхностной (3.39) нагрузок в теле возникает первая часть температурных напряжений (3.37) (первое состояние). 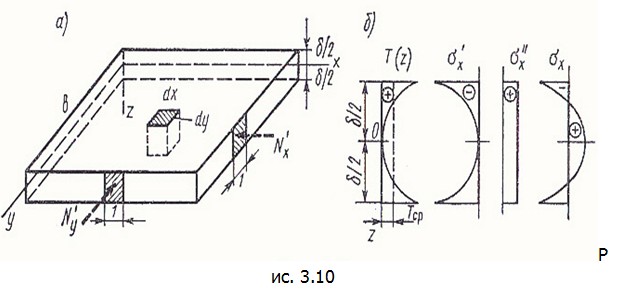
Теперь снимем упомянутые нагрузки, т.е. приложим к нему те же нагрузки, но с обратным знаком. Решая на эти силовые воздействия обычную задачу теории упругости, получим вторую часть температурных напряжений: 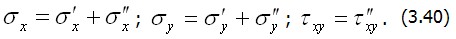
Полные перемещения u, v точек тела определяются второй частью решения (вторым состоянием). В качестве примера рассмотрим свободную от закреплений пластину (рис. 3.10, а). Пусть изменение температуры задано законом, симметричным относительно плоскости xy : 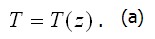
Оно может быть вызвано, например, постепенным остыванием пластины за счет равномерного оттока теплоты через ее боковые поверхности Напряжения первого состояния (3.37) при полном исключении деформации будут 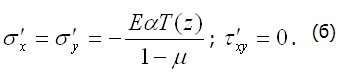
Отвечающая им объемная нагрузка (3.38) в данном случае равна нулю, так как функция T не зависит от x и y . Поверхностная нагрузка 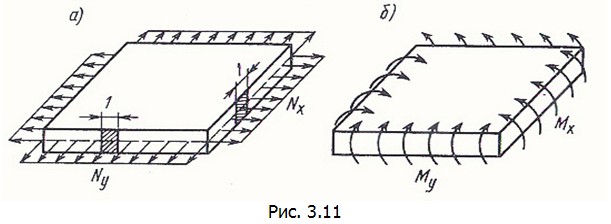
На единицу длины грани эти нагрузки дают равнодействующие силы 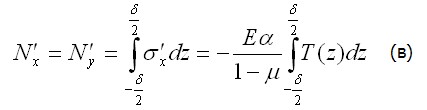
Пусть 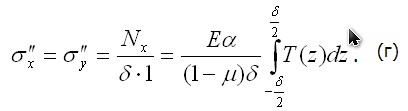
По формуле (3.40) получим суммарные напряжения 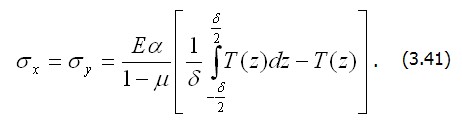
Первое слагаемое в скобках имеет смысл средней температуры 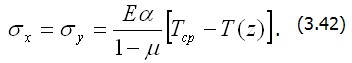
На рис. 3.10, б показаны эпюры 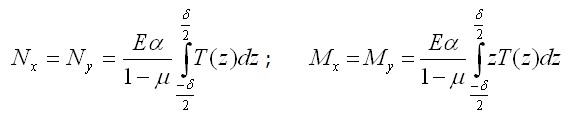
и вместо формулы (3.42 )получим 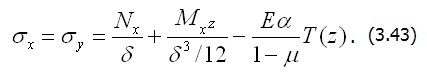
Заметим, что полученные формулы для |

 где
где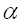 – коэффициент температурного расширения, численно равный величине относительного удлинения, вызванного изменением температуры на один градус. Такая свободная, ничем не стесненная температурная деформация не вызывает появления дополнительных напряжений в теле.
– коэффициент температурного расширения, численно равный величине относительного удлинения, вызванного изменением температуры на один градус. Такая свободная, ничем не стесненная температурная деформация не вызывает появления дополнительных напряжений в теле.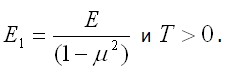
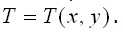 Исключим на время его деформации (в плоскости x – y ), т.е. положим
Исключим на время его деформации (в плоскости x – y ), т.е. положим 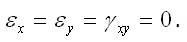 Тогда из (3.36) найдем напряжения, возникшие в теле в первом состоянии:
Тогда из (3.36) найдем напряжения, возникшие в теле в первом состоянии: (второе состояние). Действительные полные температурные напряжения в теле будут представлены суммой первого и второго состояний:
(второе состояние). Действительные полные температурные напряжения в теле будут представлены суммой первого и второго состояний: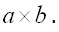 Так как T зависит от координаты z , то каждый элементарный столбик
Так как T зависит от координаты z , то каждый элементарный столбик 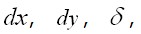 выделенный из пластина, находится в одинаковых условиях и его деформации
выделенный из пластина, находится в одинаковых условиях и его деформации 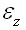 могут происходит свободно.
могут происходит свободно.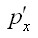 и
и 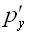 (3.39) предстанет в виде напряжений (б), приложенных к граням пластины
(3.39) предстанет в виде напряжений (б), приложенных к граням пластины 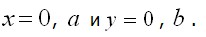
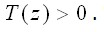 Тогда напряжения
Тогда напряжения 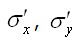 и условия
и условия 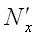 и
и 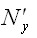 (в) будут сжимающими (рис. 3.11, б). Во втором состоянии прикладываем эти нагрузки с обратным знаком, т.е. растягивающие
(в) будут сжимающими (рис. 3.11, б). Во втором состоянии прикладываем эти нагрузки с обратным знаком, т.е. растягивающие 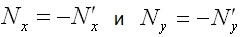 (рис. 3.11, а). От такого равномерного центрального растяжения возникают напряжения
(рис. 3.11, а). От такого равномерного центрального растяжения возникают напряжения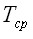 по толщине пластины: формулу (3.41) можно переписать в виде
по толщине пластины: формулу (3.41) можно переписать в виде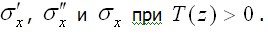 Легко видеть, что в каждом сечении напряжения
Легко видеть, что в каждом сечении напряжения 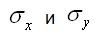 самоуравновешены, площадь этих эпюр на высоте
самоуравновешены, площадь этих эпюр на высоте  равна нулю. Подобные рассуждения можно применить и в случае, если температура
равна нулю. Подобные рассуждения можно применить и в случае, если температура 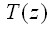 не симметрична относительно середины толщины пластины. Тогда в качестве краевых воздействий появятся кроме усилий
не симметрична относительно середины толщины пластины. Тогда в качестве краевых воздействий появятся кроме усилий 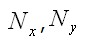 и изгибающие моменты
и изгибающие моменты 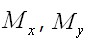 (рис. 3.11, б)
(рис. 3.11, б)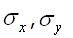 справедливы только для точек, достаточно удаленных от боковых кромок пластины, на которых фактически напряжения равны нулю. В соответствии с принципом Сен-Венана вдоль контура пластины существует зона, где распределение напряжений отличается от (3.41) и (3.43), а вне этой зоны эти формулы справедливы.
справедливы только для точек, достаточно удаленных от боковых кромок пластины, на которых фактически напряжения равны нулю. В соответствии с принципом Сен-Венана вдоль контура пластины существует зона, где распределение напряжений отличается от (3.41) и (3.43), а вне этой зоны эти формулы справедливы.