

|
3.6. Принцип Кастильяно В отличие от принципа Лагранжа, в котором состояние деформированного тела характеризуется функциями перемещений, в принципе Кастильяно состояние тела характеризуется функциями напряжений Указанные напряжения называют статически возможными или равновесными системами напряжений. Но в каждой задаче теории упругости таких систем напряжений существует бесконечно много, поскольку эта задача статически неопределима. Действительно, в три уравнения равновесия (2.3) входят шесть неизвестных функций Принцип Кастильяно из всех систем статически возможных напряжений выделяет такие, которые обеспечивают не только равновесие, но и совместимость деформаций тела и, таким образом, являются искомым единственным решением задачи теории упругости. 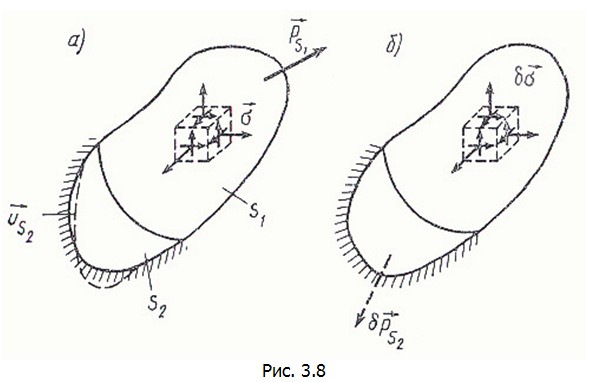
Для его формулировки рассмотрим два состояния тела: первое – с истинными напряжениями На рис. 3.8, б показано рассматриваемое тело, испытывающее самоуравновешенные напряжения В деформированном теле в качестве возможных могут быть приняты любые малые перемещения и пропорциональные им деформации, которые не нарушают его сплошности внутри тела и непрерывной связи с опорными закреплениями. Если перемещения и деформации, отвечающие истинным напряжениям, удовлетворяют этим условиям, то они могут быть приняты в качестве возможных для напряжений 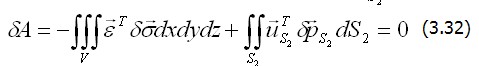
Под знаком тройного интеграла здесь стоит вариация плотности дополнительной энергии деформации 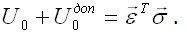
Второе слагаемое (3.32) равно вариации потенциала сил 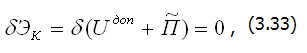
где 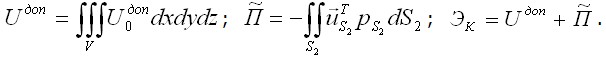
Величина Равенство (3.33) выражает принцип Кастильяно: истинные напряжения сообщают дополнительной энергии тела стационарное значение. В частном случае линейно-упругого тела и отсутствия заданных смещений 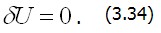 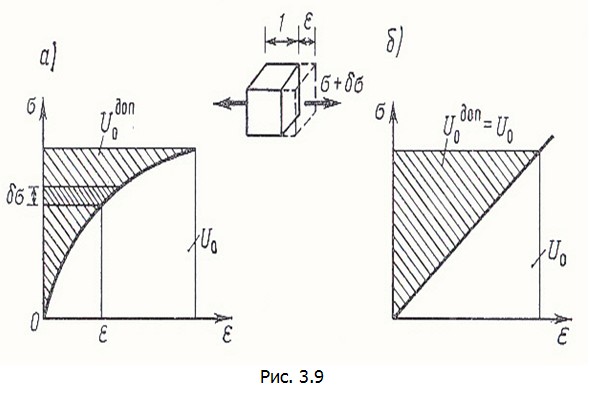
Равенство (3.34) показывает, что для истинных напряжений (или внутренних усилий) линейно-упругая система имеет потенциальную энергию деформации стационарной (для устойчивого равновесия минимальной). Поскольку энергия U численно равна работе внутренних сил, которая, в свою очередь, равна работе внешних сил деформированного тела, это положение часто называют принципом наименьшей работы. |

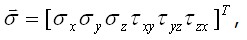 которые заведомо удовлетворяют условиям равновесия тела при данной внешней нагрузке
которые заведомо удовлетворяют условиям равновесия тела при данной внешней нагрузке 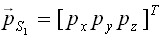 на поверхности
на поверхности 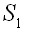 и заданным перемещениям
и заданным перемещениям 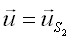 на поверхности тела
на поверхности тела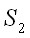 (рис. 3.8, а).
(рис. 3.8, а).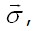 поэтому число функций
поэтому число функций 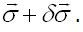 Те и другие напряжения статически возможные и, следовательно, уравновешивают внешнюю нагрузку
Те и другие напряжения статически возможные и, следовательно, уравновешивают внешнюю нагрузку 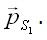 Представив себе разность этих состояний, придем к выводу о том, что напряжениям
Представив себе разность этих состояний, придем к выводу о том, что напряжениям  отвечает отсутствие нагрузки на поверхности
отвечает отсутствие нагрузки на поверхности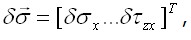 являющиеся вариациями истинных напряжений
являющиеся вариациями истинных напряжений 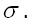 На поверхности
На поверхности 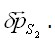 Поскольку эта система напряжений и сил равновесна, ее работа
Поскольку эта система напряжений и сил равновесна, ее работа 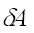 на возможных перемещениях равна нулю.
на возможных перемещениях равна нулю.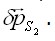 Запишем как условие совместности деформаций равенство нулю работы напряжений
Запишем как условие совместности деформаций равенство нулю работы напряжений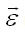 и перемещениях
и перемещениях 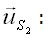
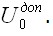 На рис. 3.9, а это показано для случая одноосного напряженного состояния и нелинейно-упругого материала. Произведение
На рис. 3.9, а это показано для случая одноосного напряженного состояния и нелинейно-упругого материала. Произведение 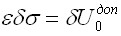 ,где
,где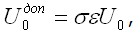 выражается площадью диаграммы деформирования материала, заштрихованной на рис. 3.9, а, б. В общем случае
выражается площадью диаграммы деформирования материала, заштрихованной на рис. 3.9, а, б. В общем случае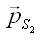 на поверхности
на поверхности 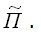 Умножая (3.32) на – 1, левую часть этого равенства запишем в виде
Умножая (3.32) на – 1, левую часть этого равенства запишем в виде 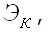 равная сумме дополнительной энергии деформации тела и потенциала реактивных сил на поверхности
равная сумме дополнительной энергии деформации тела и потенциала реактивных сил на поверхности 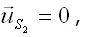 когда
когда 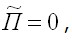 имеем
имеем 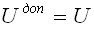 (рис. 3.9, б) и принцип Кастильяно получает вид
(рис. 3.9, б) и принцип Кастильяно получает вид