

|
3.5. Метод Ритца Условие стационарности функционала В общем случае трехмерного тела для перемещений u, v, w зададимся выражением в виде суммы: 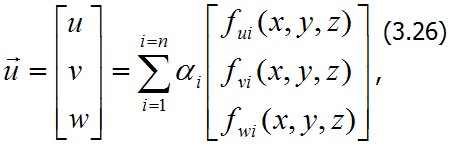
где ai,...,an – неизвестные числа (обобщенные перемещения), подлежащие определению: f1,...,fn – базисные функции, которыми мы задаемся так, чтобы они удовлетворяли условиям закрепления тела. Подставляя (3.26) в функционал (3.11) для линейно деформируемых систем, после вычисления определенных интегралов от функций fi и их производных получим его в виде квадратичной формы 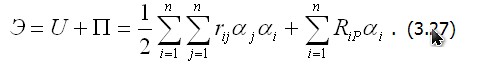
При этом можно убедиться, расписав упомянутые определенные интегралы, что всегда 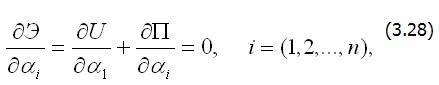
которые в случае линейно деформируемой системы с учетом (3.27) образуют систему алгебраических линейных уравнений относительно обобщенных перемещений 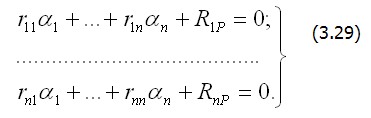
Выделим из (3.29) матрицу и вектор: 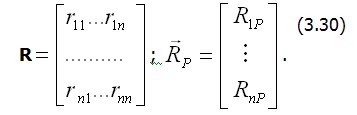
Матрица R называется матрицей жесткости, соответствующей вектору обобщенных перемещений 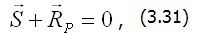
приобретают простой механический смысл, а именно: если деформированное тело (или система тел) находится в равновесии, то суммарная обобщенная сила, отвечающая каждому из возможных перемещений 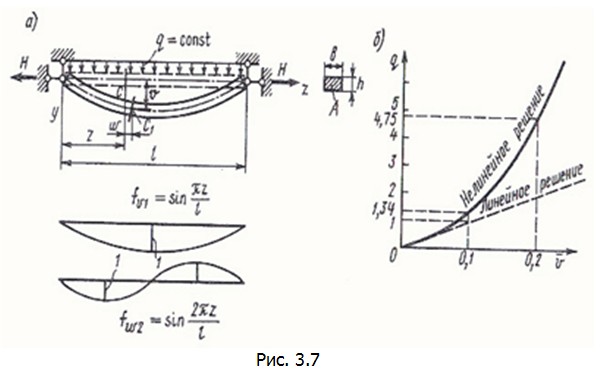
Если тело является нелинейно деформируемым, то функционал от На рис. 3.7, а показана балка, имеющая на концах шарнирно неподвижные опоры. При ее искривлении длина оси увеличивается и балка работает как на изгиб, так и на растяжение, а в горизонтальных связях возникают растягивающие силы H . Получим зависимость между нагрузкой q и прогибами v такой системы. На осевые продольные деформации 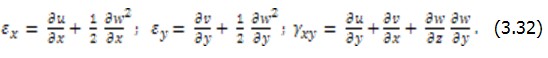
По аналогии с этими уравнениями имеем зависимость для осевой деформации 
Функционал полной энергии с учетом деформаций изгиба и растяжения получит вид 
или 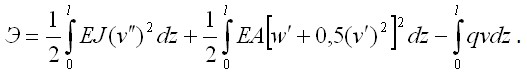
Применим метод Ритца, приняв в качестве базисных функций кривые, изображенные на рис. 3.7, а (внизу). Перемещения приближенно зададим в виде 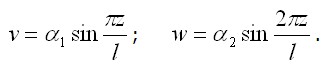
Подставив эти перемещения в выражения для энергии Э и выполнив интегрирование, получим такую функцию аргументов 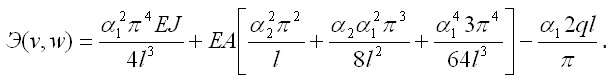
Уравнения 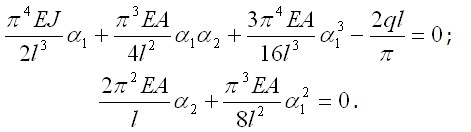
Выразив 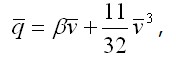
где На рис. 3.7, б сплошной линией показана кривая для балки прямоугольного сечения при В заключении этого параграфа отметим, что рассмотренные выше основы метода Ритца имеют в основном принципиальное значение. В то же время технически он реализуется в большинстве случаев в одной из форм так называемого метода конечных элементов (МКЭ), о чем более подробно сказано далее. Преимущества последнего состоят в том, что окончательные разрешающие уравнения Ритца (3.28) удается составлять, минуя операцию явного получения выражения полной энергии системы и его дифференцирования. |

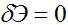 формулирует континуальную вариационную задачу с бесконечным числом компонент перемещений, определяющих разыскиваемые функции-экстремали. Идея метода, предложенного еще в начале века немецким ученым Рицем, состоит в том, чтобы от континуальной формулировки перейти к дискретной, когда функционал
формулирует континуальную вариационную задачу с бесконечным числом компонент перемещений, определяющих разыскиваемые функции-экстремали. Идея метода, предложенного еще в начале века немецким ученым Рицем, состоит в том, чтобы от континуальной формулировки перейти к дискретной, когда функционал 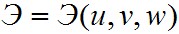 заменяется функцией
заменяется функцией 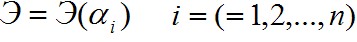 зависящей от конечного числа аргументов
зависящей от конечного числа аргументов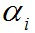 После этого задача определения экстремалей функционала перейдет в стандартную задачу исследования указанной функции дискретного числа аргументов на экстремум. Другими словами, от континуальной задачи с бесконечным числом степеней свободы в отношении формы деформирования тела мы переходим к задаче для системы с конечным числом степеней свободы.
После этого задача определения экстремалей функционала перейдет в стандартную задачу исследования указанной функции дискретного числа аргументов на экстремум. Другими словами, от континуальной задачи с бесконечным числом степеней свободы в отношении формы деформирования тела мы переходим к задаче для системы с конечным числом степеней свободы.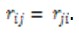 Из условия
Из условия 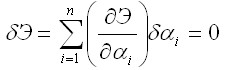 ввиду произвольности вариаций
ввиду произвольности вариаций 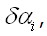 получаем n уравнений
получаем n уравнений 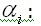
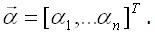 Она симметрична относительно главной диагонали, так как
Она симметрична относительно главной диагонали, так как 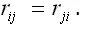 Произведение
Произведение 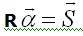 дает вектор обобщенных упругих сил. Вектор
дает вектор обобщенных упругих сил. Вектор 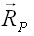 – это вектор обобщенных внешних сил. Поэтому равенства (3.28) и (3.29), которые могут быть записаны кратко в виде
– это вектор обобщенных внешних сил. Поэтому равенства (3.28) и (3.29), которые могут быть записаны кратко в виде 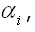 равна нулю. При этом суммарная обобщенная сила состоит из упругой силы
равна нулю. При этом суммарная обобщенная сила состоит из упругой силы  и внешней обобщенной силы
и внешней обобщенной силы 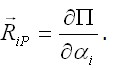
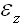 будет влиять не только продольное перемещение w , но и поперечное перемещение v , причем эта зависимость нелинейная и приближенно имеет вид уравнений:
будет влиять не только продольное перемещение w , но и поперечное перемещение v , причем эта зависимость нелинейная и приближенно имеет вид уравнений: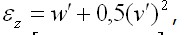 а также для продольной силы
а также для продольной силы 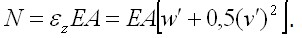 Как видим, данная система относится к разряду геометрически нелинейных систем. Плотность энергии деформации растяжения балки (на единицу длины) будет
Как видим, данная система относится к разряду геометрически нелинейных систем. Плотность энергии деформации растяжения балки (на единицу длины) будет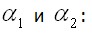
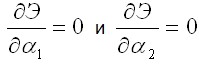 оказываются нелинейными и имеют следующий вид:
оказываются нелинейными и имеют следующий вид: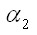 через
через 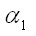 из второго уравнения
из второго уравнения 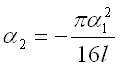 и подставив его в первое уравнение, получим искомую зависимость
и подставив его в первое уравнение, получим искомую зависимость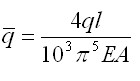 – безразмерная нагрузка;
– безразмерная нагрузка;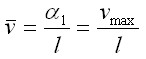 – безразмерный (относительный) прогиб в середине пролета:
– безразмерный (относительный) прогиб в середине пролета: 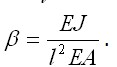
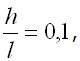 для которой
для которой 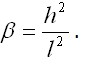 Так же пунктиром изображен результат линейного решения, когда учитывается только деформация изгиба. Как видим, при прогибе, имеющем порядок высоты сечения балки
Так же пунктиром изображен результат линейного решения, когда учитывается только деформация изгиба. Как видим, при прогибе, имеющем порядок высоты сечения балки 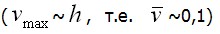 и более, не учет нелинейной работы системы приводит к существенным погрешностям. Этот вывод в еще большей мере характерен также для гибких пластин и оболочек.
и более, не учет нелинейной работы системы приводит к существенным погрешностям. Этот вывод в еще большей мере характерен также для гибких пластин и оболочек.