|
3.4 Связь между вариационной и дифференциальной формулировками задач теории упругости
Эта связь в математике выражается в том, что каждой вариационной формулировке типа 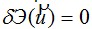 может быть поставлена в соответствие формулировка в форме дифференциальных уравнений относительно разыскиваемых функций может быть поставлена в соответствие формулировка в форме дифференциальных уравнений относительно разыскиваемых функций 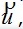 называемых уравнениями Эйлера для функционала Э . Покажем эту связь и процесс получения уравнений Эйлера на простом примере.
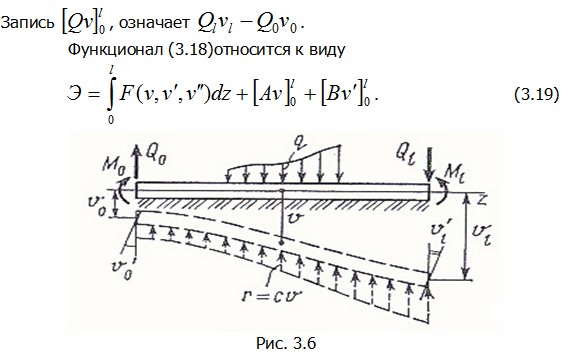
Запишем функционал полной энергии для балки, лежащей на винклеровом основании с коэффициентом жесткости с (рис. 3.6): называемых уравнениями Эйлера для функционала Э . Покажем эту связь и процесс получения уравнений Эйлера на простом примере.
Запишем функционал полной энергии для балки, лежащей на винклеровом основании с коэффициентом жесткости с (рис. 3.6):
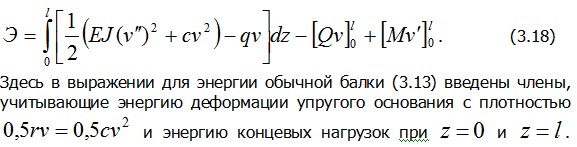
Операция варьирования аналогична операции дифференцирования. При получении вариации 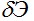 будем рассматривать выражение F как сложную функцию от v . В результате получим будем рассматривать выражение F как сложную функцию от v . В результате получим
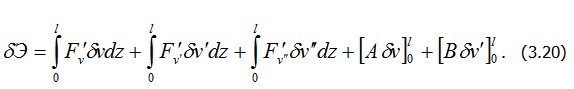
Здесь штрихом при F отмечается частная производная выражения 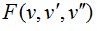 по аргументу, указанному в нижнем индексе. Условием по аргументу, указанному в нижнем индексе. Условием 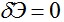 в форме (3.20) пользоваться для определения v=v(z) неудобно, так как оно содержит не только произвольную функцию в форме (3.20) пользоваться для определения v=v(z) неудобно, так как оно содержит не только произвольную функцию 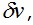 , но и ее производные. Поэтому преобразуем (3.20) так, чтобы из-под интегралов были исключены производные , но и ее производные. Поэтому преобразуем (3.20) так, чтобы из-под интегралов были исключены производные 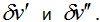
Для этого интегрируем второе слагаемое по частям один раз, а третье – два раза. В результате получим
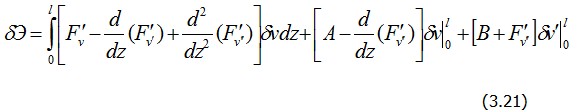
Теперь из условия 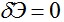 ввиду произвольности функции ввиду произвольности функции 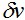 следует равенство нулю выражения в прямых скобках под интегралом, а именно: следует равенство нулю выражения в прямых скобках под интегралом, а именно:
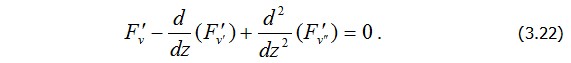
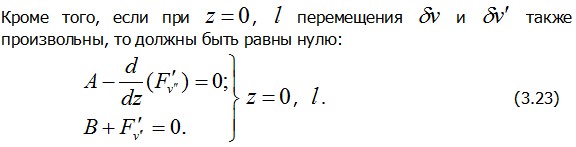
Равенство (3.22) и является дифференциальным уравнением Эйлера для функционала (3.19), а (3.23) – его граничными условиями.
Применительно к балке на упругом основании (3.18) имеем
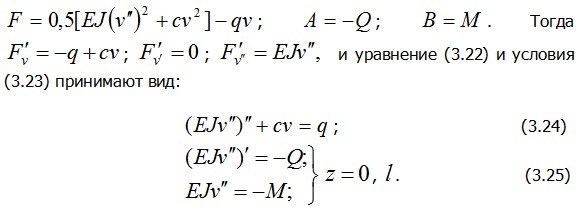
Таким образом, вариационное уравнение 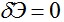 в интегральной форме выражающее условия равновесия деформированного тела, эквивалентно и включает в себя соответствующие дифференциальные уравнения равновесия теории упругости вместе с условиями равновесия на поверхности тела (граничными условиями). Указанные дифференциальные уравнения служат уравнениями Эйлера функционала Э.При этом если последний будет выражен только через три функции перемещений в интегральной форме выражающее условия равновесия деформированного тела, эквивалентно и включает в себя соответствующие дифференциальные уравнения равновесия теории упругости вместе с условиями равновесия на поверхности тела (граничными условиями). Указанные дифференциальные уравнения служат уравнениями Эйлера функционала Э.При этом если последний будет выражен только через три функции перемещений 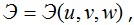 то, следуя по пути, показанному в примере, мы придем к уравнениям Эйлера в форме уравнений Ляме (2.30), т.е. уравнений равновесия, записанных в перемещениях. Отметим, что в этом случае при исключении из уравнения то, следуя по пути, показанному в примере, мы придем к уравнениям Эйлера в форме уравнений Ляме (2.30), т.е. уравнений равновесия, записанных в перемещениях. Отметим, что в этом случае при исключении из уравнения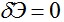 частных производных функций частных производных функций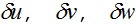 потребуется операция, аналогичная интегрированию по частям – переход от интеграла по объему к интегралу по поверхности по формуле Грина. На этих преобразованиях останавливаться не будем. потребуется операция, аналогичная интегрированию по частям – переход от интеграла по объему к интегралу по поверхности по формуле Грина. На этих преобразованиях останавливаться не будем.
Вариационная формулировка задачи теории упругости используется главным образом в двух случаях. В первом на основе уравнения 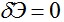 строятся численные методы решения этой задачи (метод Ритца, метод конечных элементов и т.п.). Все эти методы относят к классу прямых методов решения задач теории упругости, не требующих в явной форме использования дифференциальных уравнений. строятся численные методы решения этой задачи (метод Ритца, метод конечных элементов и т.п.). Все эти методы относят к классу прямых методов решения задач теории упругости, не требующих в явной форме использования дифференциальных уравнений.
Второй характерный случай применения вариационного подхода – это получение дифференциальных уравнений и граничных условий рассматриваемой задачи, как уравнений Эйлера соответствующего функционала. Такой путь оказывается оправданным для тел сложной формы и структуры (например, многослойные оболочки и др.), а также при переходе от одной системы координат к другой (от декартовой системы к полярной, криволинейной и другим системам).
Далее ->
|





