|
3.3. Вариационный принцип Лагранжа
Применим к деформированному телу принцип возможных перемещений Лагранжа. Он выражает условие равновесия системы внутренних и внешних сил. Согласно этому принципу, если 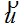 истинные перемещения точек тела, при которых имеет место равновесие упомянутых систем сил, то работа этих сил на произвольном бесконечном малом изменении перемещений истинные перемещения точек тела, при которых имеет место равновесие упомянутых систем сил, то работа этих сил на произвольном бесконечном малом изменении перемещений 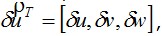 допускаемом связями тела, должна быть равна нулю. Бесконечно малые функции допускаемом связями тела, должна быть равна нулю. Бесконечно малые функции  называются вариациями функций u, v, w. называются вариациями функций u, v, w.
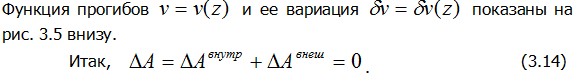
Но приращения работы внутренних Aвнутр и внешних сил Aвнешс точностью до знака представляют приращения соответствующих потенциалов ΔU и ΔП. Поэтому 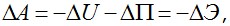 откуда следует, что для истинных перемещений откуда следует, что для истинных перемещений 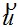 изменение полной энергии ΔЭ. вызванное вариациями изменение полной энергии ΔЭ. вызванное вариациями 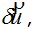 должно быть равно нулю: должно быть равно нулю:
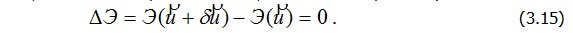
Левая часть (3.15) в общем случае сложно зависит от приращения перемещений 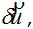 поэтому представим ее виде суммы, в которой каждое слагаемое зависит от соответствующей степени поэтому представим ее виде суммы, в которой каждое слагаемое зависит от соответствующей степени 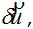 называется первой вариацией функционала называется первой вариацией функционала 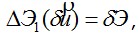 второе слагаемое есть вторая вариация
второе слагаемое есть вторая вариация 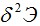 и т.д. устремляя в (3.16) и т.д. устремляя в (3.16) 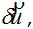 к нулю и отбрасывая все слагаемые, кроме первого, как бесконечно малые более высокого порядка малости, приходим к равенству к нулю и отбрасывая все слагаемые, кроме первого, как бесконечно малые более высокого порядка малости, приходим к равенству  Из курса математики известно, что равенство нулю первой вариации функционала (3.17) является необходимым условием локального экстремума этого функционала. Оно выражает тот факт, что в локальной зоне изменения функций-аргументов функционал с точностью до бесконечно малых первого порядка сохраняет неизменное (стационарное) значение. Из курса математики известно, что равенство нулю первой вариации функционала (3.17) является необходимым условием локального экстремума этого функционала. Оно выражает тот факт, что в локальной зоне изменения функций-аргументов функционал с точностью до бесконечно малых первого порядка сохраняет неизменное (стационарное) значение.

Принцип вариации перемещений (принцип Лагранжа) может быть сформулирован так : для истинных перемещений u , v , w функционал полной энергии деформированного тела имеет экстремальное (стационарное) значение, т.е. его первая вариация равна нулю (3.17).
Таким образом, при заданной нагрузке на тело надо найти такие функции u, v , w , при которых выполняется условие 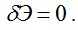 . Тем самым будут найдены истинные перемещения тела и решена задача теории упругости (в перемещениях). В этом и состоит вариационная формулировка задачи теории упругости с помощью принципа Лагранжа. Механически оно в интегральной форме выражает условия равновесия деформированного тела.
. Тем самым будут найдены истинные перемещения тела и решена задача теории упругости (в перемещениях). В этом и состоит вариационная формулировка задачи теории упругости с помощью принципа Лагранжа. Механически оно в интегральной форме выражает условия равновесия деформированного тела.
Далее ->
|





