|
2.5 Понятие о методе напряжений и методе перемещений Выпишем еще раз в сокращенной форме основные уравнения теории упругости, а именно: I – статические, II – геометрические и III – физические: Вместо уравнений Коши II (2.16) могут быть использованы полученные из них уравнения совместности деформаций Сен-Венана (2.22), а вместо закона Гука в прямой форме III (2.20) – равенства (2.24), представляющие тот же закон, но в обратной форме. Поэтому вместо (2.26) можно написать эквивалентную систему уравнений в виде где II* и III* - преобразование уравнения II и III из (2.26). Легко видеть, что равенства (2.26) представляют замкнутую систему уравнений, в которой число уравнений (3+6+6=15) совпадает с числом неизвестных (6 напряжений + 6 деформаций + 3 перемещения). Следовательно, при задании необходимых граничных условий на поверхности тела в виде заданных перемещений или заданных поверхностных нагрузок система линейных уравнений (2.26) может быть решена. Условимся, что данное тело при отсутствии внешних нагрузок в естественном состоянии не имеет внутренних напряжений и закреплено от смещений как жесткое целое. Предположим, что удалось найти некоторую систему 15 функций Отметим одну особенность уравнений (2.26) . Если ставится так называемая обратная задача теории упругости, когда требуется найти напряжения и деформации по заданным перемещениям Отметим, что в прямой задаче получить точные решения уравнений (2.26) в общем случае очень сложно. В курсе теории упругости исследуются возможные пути упрощения этой задачи или ее приближенного решения. Один из путей упрощения состоит в том, что определяются не сразу все 15 функций, а лишь часть из них, принимаемые за основные. Рассмотрим в связи с этим два характерных подхода, составляющих так называемые: метод напряжений (решение в напряжениях) и метод перемещений (решение в перемещениях). В методе напряжений за основные неизвестные принимаются шесть функций, составляющих вектор напряжений: По аналогии со сказанным, и в методе напряжений в качестве основных разрешающих уравнений принимаются геометрические уравнения в форме уравнений Сен-Венана II* - уравнений совместности деформаций. Шесть указанных уравнений надо выразить через шесть неизвестных функций Пользуясь сокращенной записью уравнений (2.26) и (2.27), наметим путь указанного преобразования. Подставляя в II* значение деформаций, выраженных через напряжения Напряжения Если принять объемные силы Оператор После того как из уравнений (2.29) найдены напряжения В методе перемещений за основные неизвестные принимаются три функции: u,v,w– компоненты перемещений точек тела, а в качестве разрешающих уравнений – три уравнения равновесия I. Их преобразуют так, чтобы вместо напряжений в них входили перемещения. По закону Гука III* с учетом II имеет Преобразования по (2.30) приводят к трем уравнениям равновесия, выраженным через перемещения (уравнения Ляме): Если искомая деформация тела вызывается заданными принудительными смещениями какой-либо части его поверхности, то граничные условия для уравнений (2.26) формулируют, приравнивая функции u,v,w на границе заданных перемещениям. Сложнее, если на тело действует заданная поверхностная нагрузка Помимо двух основных рассмотренных методов решения задач теории упругости в напряжениях и в перемещениях часто используется смешенная форма решения, когда разрешающие уравнения составляются частично относительно перемещений, а частично относительно напряжений. Такой прием применяется в задачах расчета оболочек. |
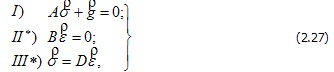
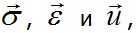которые удовлетворяют уравнениям (2.26) и заданным на поверхности граничным условиям. Тогда можно утверждать, что эти функции выражают точное и единственное решение задачи о напряженно-деформированном состоянии рассматриваемого тела. В этом состоит так называемая теорема о единственности решения задачи теории упругости. Ее доказывают, используя линейность уравнений (2.26) (на чем останавливаться не будем).
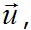а также установить нагрузки 
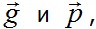вызывающие эти перемещения, то ее решение с помощью (2.26) выполняется без затруднений. Действительно, по заданным 
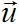и по формулам Коши II вычисляем деформации 
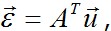далее по закону Гука III* находим напряжения 
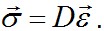Из уравнений равенства I получим требующиеся объемные нагрузки 
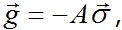а с помощью условий на поверхности (2.9) находим поверхностные нагрузки 
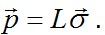Но рассмотренная обратная задача редко имеет практическое применение. Основные трудности представляет решение прямой задачи теории упругости, а именно определение напряжений, деформаций и перемещений тела по заданным объемным нагрузкам, а также силовым или кинематическим воздействиям, приложенным на его поверхности. В этом случае необходимо интегрировать дифференциальные уравнения в частных производных (I и II или II*), входящие в состав общих уравнений (2.26).
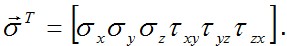Задача их определения является, как указывалось, статически неопределимой. Из курса сопротивления материалов известно, что при решении статически неопределенных задач «лишние» внутренние усилия определяются из так называемых уравнений деформаций, выражающих условия совместности деформирования элементов конструкции и опорных связей.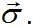
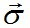по закону Гука III, получим первую строку равенств:
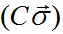надо понимать условно. Вместо произведения элементов В и 
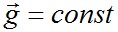или равные нулю и соответствующим образом использовать при указанных преобразованиях уравнения равновесия, то шесть уравнений совместности деформаций, выраженные через напряжения, приводятся к виду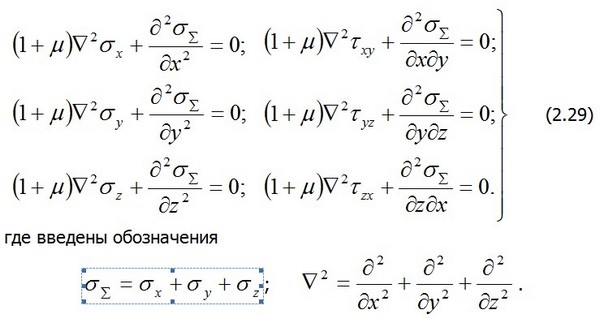 
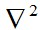называют гармоническим оператором Лапласа. Уравнения (2.29) получены Бельтрами и носят его имя. Аналогические уравнения для произвольных объемных сил получены Мичеллом.
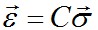и далее путем интегрирования уравнений Коши II (что заведомо возможно, так как 
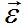удовлетворяют условиям совместимости деформаций) определяем перемещения 
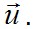В такой последовательности определяются все 15 неизвестных функций по методу напряжений.
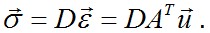Подставив это значение 
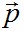и условия на поверхности выражаются равенствами (2.8) или в сокращенной форме (2.9) 
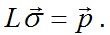Последние надо преобразовать, заменив в них напряжения 
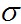через перемещения 
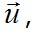что делается по той же схеме, что и в уравнениях (2.30).