|
3.1. Общие замечания Рассмотренные в предыдущей главе уравнения механики деформируемого тела вместе с условиями на поверхности образуют законченную формулировку задачи теории упругости в дифференциальной форме. Однако это не единственная возможная формулировка задачи об отыскании напряженно-деформированного состояния тела. Оказывается, задачу определения функций В данной главе прежде всего познакомимся с двумя основными принципами Лагранжа и Кастильяно, а также с некоторыми другими принципами. Укажем на связь этих принципов и вариационной формулировки задачи упругости с дифференциальной формой этой задачи. На основе вариационных принципов в механике твердых деформируемых тел строятся в настоящее время мощные приближенные методы анализа работы деформируемых тел и систем таких тел. Некоторые из них приводятся ниже и будут рассмотрены далее. |
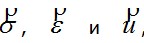характеризующих это состояние, можно свести к определенному интегралу того или иного вида от этих функций, называемому функционалом, а сами функции, отражающие действительное состояние тела, найти из условия экстремума этого функционала. Математический аппарат такого подхода изучается в разделе математики, называемом вариационным исчислением. Поэтому положения, формулирующие свойства таких функционалов в теории упругости, получили название вариационных принципов.
