|
2.4 Физические уравнения теории упругости Ещё рассматриваются физические уравнения теории упругости, которые являются соотношениями обобщённого закона Гука: где Е и G – модули упругости при растяжении и сдвиге, а так, что независимых постоянных упругости для указанного материала только две. В сокращенной форме уравнения (2.16) запишем в виде где матрица упругой податливости С с учетом (2.16) получит вид: Уравнения (2.16) дают возможность вычислить деформации, если известны напряжения. Назовем их законом Гука в прямой форме. В ходе решения задач теории упругости возникает необходимость в обратных соотношениях, когда напряжения выражены через деформации. Для этого надо разрешить уравнения (2.16) относительно напряжений. Запишем первую строку (2.16) в виде Из курса сопротивления материалов известно следующее выражение для относительной объемной деформации элемента: Заменяя в (2.20) сумму Через В сокращенной форме уравнения (2.22) представим в виде Где D матрица жесткости элемента материала Эта матрица играет основную роль при методе расчета 15 уравнений напряженно-деформированного состояния твердого тела методом конечных элементов. |
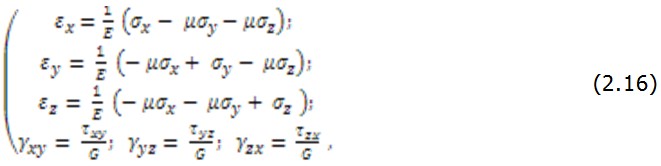
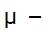– коэффициент Пуассона. Для изотропного материала они связаны зависимостью
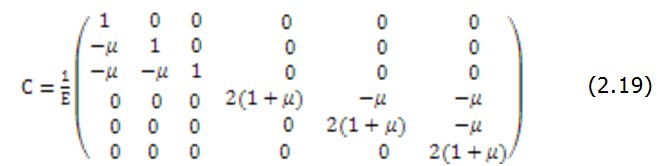
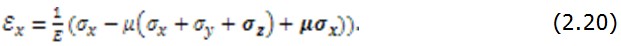
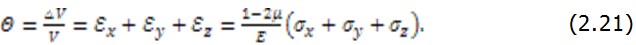
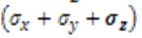на величину, найденную из (2.21), и разрешая (2.20), получим закон Гука в обратной форме, т.е. напряжения, выраженные через деформации.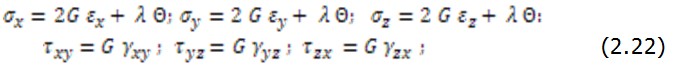 
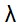обозначена константа, называемая параметром Ляме:
