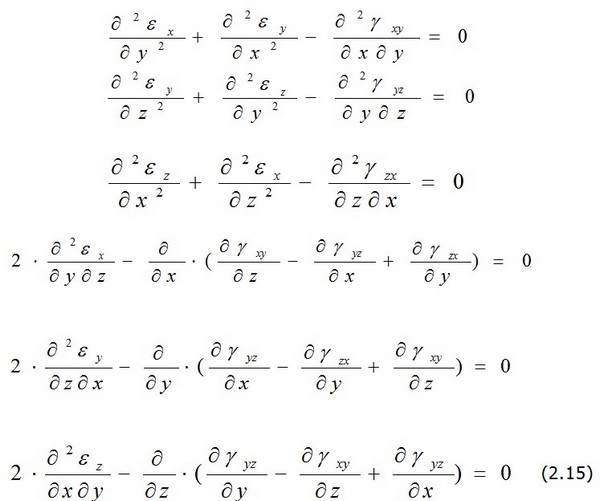|
2.3 Уравнения совместности деформаций
Если даны три компоненты непрерывного поля перемещений 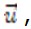 , то по ним легко определяются соответствующие шесть компонент поля деформаций по формулам Коши (2.14). Сложнее обстоит дело с обратной постановкой задачи. Если заданы шесть компонент деформаций , то по ним легко определяются соответствующие шесть компонент поля деформаций по формулам Коши (2.14). Сложнее обстоит дело с обратной постановкой задачи. Если заданы шесть компонент деформаций 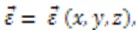 то заранее нельзя утверждать, что им соответствует непрерывное поле перемещений. Деформации, которым отвечает непрерывное поле перемещений, называются совместными деформациями. В противном случае деформации называют несовместными. то заранее нельзя утверждать, что им соответствует непрерывное поле перемещений. Деформации, которым отвечает непрерывное поле перемещений, называются совместными деформациями. В противном случае деформации называют несовместными.
Для того чтобы деформации были совместными, они должны быть взаимосвязаны некоторыми соотношениями, которые называются уравнениями совместности деформаций. Необходимость их существования можно проиллюстрировать следующим простым рассуждением.
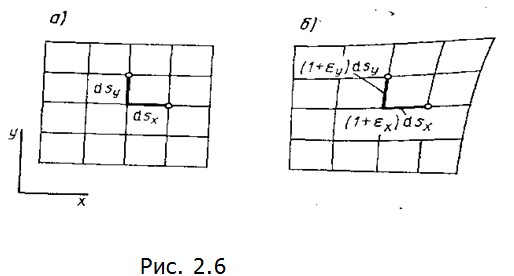
На рис. 2.6, а показано тело до деформации, разбитое на части сеткой ортогональных прямых. Зададим в этом теле поле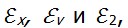 в результате чего прямые получат некоторые удлинения. Так, вместо dsx будем иметь в результате чего прямые получат некоторые удлинения. Так, вместо dsx будем иметь 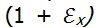 dsx. Тело деформируется, как это показано на рис. 2.6, б. При этом возникают и углы сдвига как изменения прямых углов, зависящие от dsx. Тело деформируется, как это показано на рис. 2.6, б. При этом возникают и углы сдвига как изменения прямых углов, зависящие от 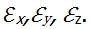 . Очевидно, наоборот, задавая . Очевидно, наоборот, задавая 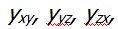 в непрерывно деформируемом теле будем иметь некоторые зависящие от них линейные деформации в непрерывно деформируемом теле будем иметь некоторые зависящие от них линейные деформации 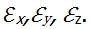 В случае произвольного и независимого задания удлинений и углов сдвига деформированные элементы тела не удастся сложить в сплошное тело. Поэтому упомянутые уравнения также называются уравнениями сплошности или неразрывности. В случае произвольного и независимого задания удлинений и углов сдвига деформированные элементы тела не удастся сложить в сплошное тело. Поэтому упомянутые уравнения также называются уравнениями сплошности или неразрывности.
Рассмотрим случай малых деформаций и перемещений, когда справедливы линейные уравнения. Для вывода уравнений совместности исключим из уравнений Коши (2.14) перемещения и, v, w. Уравнения совместности имеют вид:
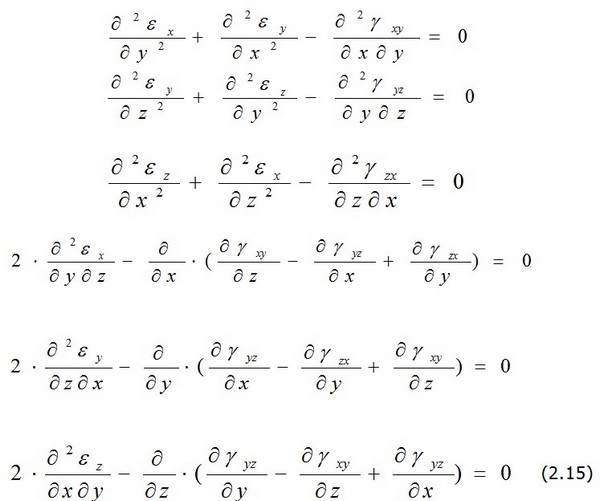
Далее ->
|



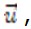 , то по ним легко определяются соответствующие шесть компонент поля деформаций по формулам Коши (2.14). Сложнее обстоит дело с обратной постановкой задачи. Если заданы шесть компонент деформаций
, то по ним легко определяются соответствующие шесть компонент поля деформаций по формулам Коши (2.14). Сложнее обстоит дело с обратной постановкой задачи. Если заданы шесть компонент деформаций 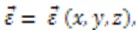 то заранее нельзя утверждать, что им соответствует непрерывное поле перемещений. Деформации, которым отвечает непрерывное поле перемещений, называются совместными деформациями. В противном случае деформации называют несовместными.
то заранее нельзя утверждать, что им соответствует непрерывное поле перемещений. Деформации, которым отвечает непрерывное поле перемещений, называются совместными деформациями. В противном случае деформации называют несовместными.
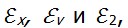 в результате чего прямые получат некоторые удлинения. Так, вместо dsx будем иметь
в результате чего прямые получат некоторые удлинения. Так, вместо dsx будем иметь 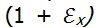 dsx. Тело деформируется, как это показано на рис. 2.6, б. При этом возникают и углы сдвига как изменения прямых углов, зависящие от
dsx. Тело деформируется, как это показано на рис. 2.6, б. При этом возникают и углы сдвига как изменения прямых углов, зависящие от 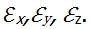 . Очевидно, наоборот, задавая
. Очевидно, наоборот, задавая 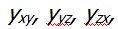 в непрерывно деформируемом теле будем иметь некоторые зависящие от них линейные деформации
в непрерывно деформируемом теле будем иметь некоторые зависящие от них линейные деформации