

|
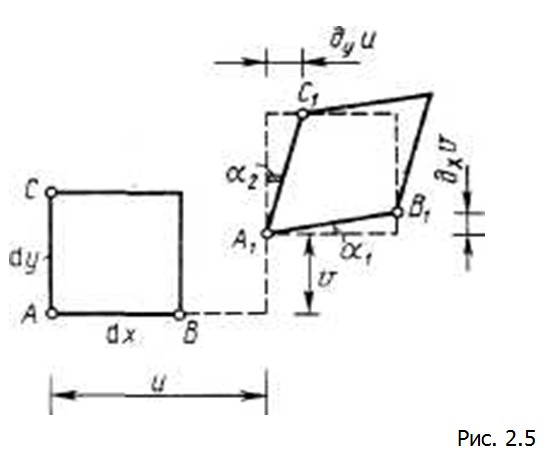
2.2 Геометрические уравнения Показано, что геометрическая деформация тела характеризуется двумя группами функций. Первая группа – это компоненты перемещений точек Рис. 2.3 Вторая группа – это относительные деформации элементарных параллелепипедов dx, dy, dz, на которые мысленно можно расчленить тело. В каждой точке они составляют тензор деформаций: шесть различных компонент которого как функции координат составляют тензор деформаций. Геометрические уравнения устанавливают зависимости между перемещениями и деформациями. Для их вывода будем считать функции Для определения деформации Для определения уху рассмотрим проекцию параллелепипеда dx, dy, dz на плоскость х — у. На рис. 2.5 показано положение этого параллелепипеда до деформации CAB и С1А1В1 после деформации. Угол сдвига уху — это малое изменение прямого угла CAB. При его определении ввиду малости перемещений и деформаций не будем учитывать влияние перемещений w и изменение длины ребер параллелепипеда, т. е. считать, что параллелепипед сначала получил поступательное перемещение точки А (хА, уА) в точку A1 (хА + u, уА + v) как жесткое целое, а затем произошел сдвиг за счет поворота его граней на малые углы
Таким образом, имеем угол сдвига в плоскости x – y Для получения формул, выражающих
Геометрические уравнения (2.14) носят название уравнений Коши. Для записи уравнений Коши в сокращенном виде введем векторы деформаций и перемещений Тогда уравнения (2.14) можно записать в виде где Уравнения деформаций (2.14) получились в виде линейных соотношений между перемещениями |

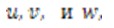 параллельные соответственно осям
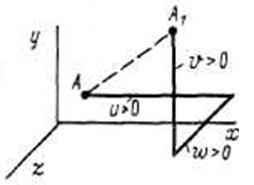
параллельные соответственно осям 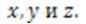 Для точки А такие перемещения показаны на рисунке 2.3. Условимся далее считать
Для точки А такие перемещения показаны на рисунке 2.3. Условимся далее считать 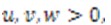 если они совпадают с положительным направлением соответствующей оси координат, и наоборот. Три функции
если они совпадают с положительным направлением соответствующей оси координат, и наоборот. Три функции 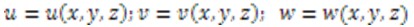 определяют поле перемещений деформируемого тела.
определяют поле перемещений деформируемого тела.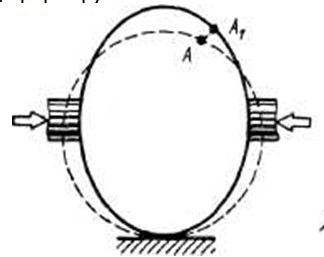
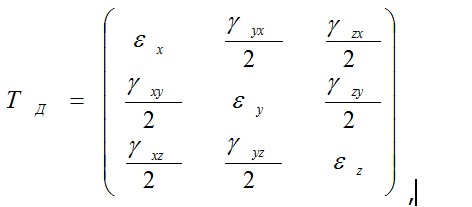
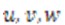 заданными, а через них выразим деформации.
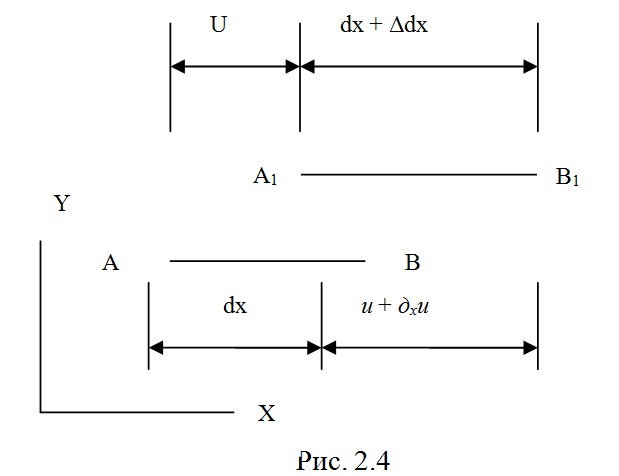
заданными, а через них выразим деформации.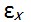 рассмотрим отрезок А В длиной dx (рис. 2.4). Для малых перемещений и деформаций примем, что на изменение длины отрезка влияет лишь перемещение u, а его малый наклон, в общем случае вызываемый перемещениями
рассмотрим отрезок А В длиной dx (рис. 2.4). Для малых перемещений и деформаций примем, что на изменение длины отрезка влияет лишь перемещение u, а его малый наклон, в общем случае вызываемый перемещениями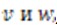 ,не изменяет его длины. Поэтому на рис. 2.4 изображено лишь поступательное перемещение отрезка. Обозначим
,не изменяет его длины. Поэтому на рис. 2.4 изображено лишь поступательное перемещение отрезка. Обозначим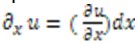 частный дифференциал (линейная часть приращения) функции u при изменении координаты х на х + dx. Из рис. 2.4 видно, что
частный дифференциал (линейная часть приращения) функции u при изменении координаты х на х + dx. Из рис. 2.4 видно, что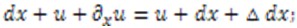 следовательно,
следовательно, 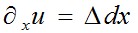 и
и 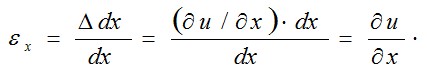
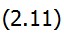
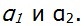 Следовательно,
Следовательно, 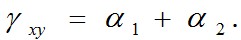 Так как частные дифференциалы
Так как частные дифференциалы 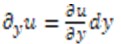 и
и  то
то 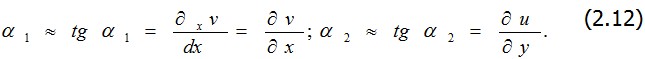
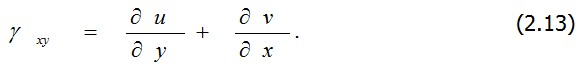
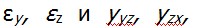 надо в выражениях (2.11), (2.13) для
надо в выражениях (2.11), (2.13) для 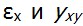 последовательно заменить обозначения координат и компонент перемещений
последовательно заменить обозначения координат и компонент перемещений 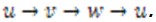 Эта операция обычно называется круговой подстановкой обозначений. В результате получим линейные и угловые деформации в виде
Эта операция обычно называется круговой подстановкой обозначений. В результате получим линейные и угловые деформации в виде
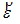 и
и 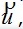 аналогичные векторам (2.5)
аналогичные векторам (2.5)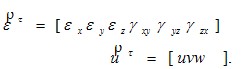
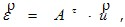
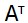 - транспонированная матрица А (2.7), фигурирующая в уравнениях равновесия (2.6).
- транспонированная матрица А (2.7), фигурирующая в уравнениях равновесия (2.6).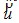 и деформациями
и деформациями