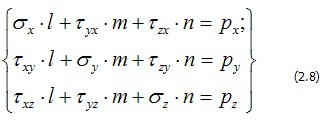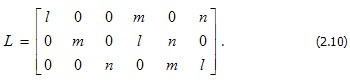|
2.1 Уравнения равновесия элемента тела (статические уравнения)
На рис. 2.1, а) показан элементарный параллелепипед, на гранях которого указаны нормальные и касательные напряжения, которыми он взаимодействует с соседними элементами в общем случае. Ввиду бесконечной малости параллелепипеда на этом рисунке принято, что напряжения во всем его объеме остаются неизменными (однородное напряженное состояние). Поэтому здесь на параллельных гранях предполагаются равные, но противоположно направленные напряжения. По существу, это напряжения на трех взаимно ортогональных площадках, проведенных через рассматриваемую точку. Они составляют тензор напряжений в данной точке.
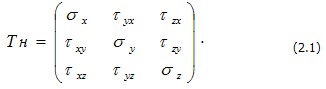
В предыдущей главе они использовались для анализа напряжен¬ного состояния в точке, т. е. для изучения законов изменения напряжений в зависимости от ориентации площадки, проведенной через точку.
В данном случае задача иная. Все компоненты тензора напряжений (2.1) в сплошной среде непрерывно изменяются от точки к точке тела, т. е. они являются непрерывными функциями координат σx=σx(x, y, z); σy=σy(x, y,z);...τxz=τzx(x, y,z) или в сокращенной форме TH=TH(x, y, z) (2.2)

Функции тензора напряжений определяют непрерывное поле напряжений в объеме тела, и необходимо выяснить, каким условиям должны быть подчинены эти функции, чтобы каждый элемент тела в своем взаимодействии с соседними элементами был в равновесии.
Поэтому на рисунке 2.1, б) изображена уточненная картина действия напряжений на гранях параллелепипеда. Если на левой грани элемента, проходящей через рассматриваемую точку А, принять напряжение σx, то на правой грани, имеющей координату х + dx, функция σx получит приращение, равное частному дифференциалу этой функции по аргументу х, т. е. будет 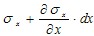 . С учетом сказанного на рис.2.1, б показаны все компоненты напряжений, параллельные оси х. . С учетом сказанного на рис.2.1, б показаны все компоненты напряжений, параллельные оси х.
Как и в § 1.1, предположим, что на тело действует некоторая объемная внешняя нагрузка, например его вес или сила инерции, компоненты интенсивности которой обозначаются X, Y, Z. Соответствующая элементарная сила в рассматриваемой точке получается как произведение интенсивности X, Y, Z на объем параллелепипеда dxdydz. Элементарные силы на поверхностях граней параллелепипеда получаем как произведение напряжений или их дифференциалов на площади граней. Учитывая, что силы σчdydz, τyxdxdz и τzxdxdy на параллельных гранях взаимно уравновешены, сумму проекций на ось х всех сил, действующих на элемент (рис. 2.1, б), составим в виде
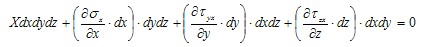
Сократив на dxdydz, получим первую строку из следующих трех дифференциальных уравнений равновесия:

Вторая и третья строки составлены аналогично первой и выражают равенство нулю сумм проекций на оси у и z.
Приравняем нулю сумму моментов сил, действующих на параллелепипед, относительно оси, проходящей через его центр параллельно оси z, получим
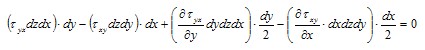
Отбросив последние два слагаемых, как бесконечно малые более высокого порядка и сокращая на dxdydz, получаем τxy=τyx . Таким образом, в дополнение к (2.3) можем написать равенства, выражающие известный закон парности касательных напряжений:
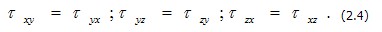
Введем сокращенную запись уравнений (2.3), используя матричную форму представления систем уравнений. Обозначим вектор напряжений 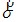 и вектор интенсивности объемной нагрузки и вектор интенсивности объемной нагрузки
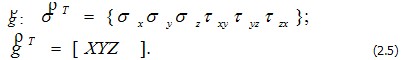
Здесь и далее верхний индекс «т» обозначает транспонирование вектора, что позволяет для сокращения записать его не в столбец, а в строку. Уравнения (2.3) условно можно представить в виде:

где матрица А состоит из элементов, выражающих соответствующие операторы дифференцирования:

Сокращенной записью (2.6) будем пользоваться в дальнейшем вместо развернутого представления (2.3).
Три дифференциальных уравнения (2.3) содержат шесть неизвестных функций напряжений σx, σy,..., τzx , которые, естественно, не могут быть однозначно определены путем интегрирования лишь уравнений равновесия. Поэтому далее потребуется дополнить эти уравнения другими (уравнениями деформаций и физическими уравнениями). В этом смысле говорят, что задача определения напряжений в деформируемом теле является статически неопределимой.
Интегрирование уравнений (2.3) дает бесконечное множество статически возможных полей напряжений Тн (х, у, z), т. е. напряжений, удовлетворяющих условиям равновесия. Использование других упомянутых групп уравнений позволяет выделить из всех статически возможных истинное поле напряжений.
Сформулируем теперь условия на поверхности тела как граничные условия для дифференциальных уравнений (2.3). Они выражают равновесие между поверхностной нагрузкой 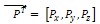 и напряжениями в произвольной точке поверхности тела. На рис. 2.2, а) показан элементарный тетраэдр, выделенный у поверхности тела сечениями, параллельными координатным плоскостям, и плоскостью, касательной к поверхности. Ориентацию последней определяет нормаль , направляющие косинусы которой обозначим: и напряжениями в произвольной точке поверхности тела. На рис. 2.2, а) показан элементарный тетраэдр, выделенный у поверхности тела сечениями, параллельными координатным плоскостям, и плоскостью, касательной к поверхности. Ориентацию последней определяет нормаль , направляющие косинусы которой обозначим:
` 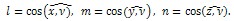
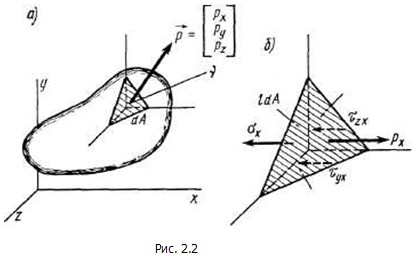
На рис. 2.2, б изображен тот же тетраэдр, что и на рисунке 1.3, но с указанием на его гранях компонент напряжений и интенсивности поверхностной нагрузки. Для простоты на чертеже показаны лишь компоненты, параллельные оси х. Там же указаны площади граней ldA ,mdA, ndA, где dA— площадь его наклонной грани. Если теперь составить условия равновесия тетраэдра в виде сумм проекций на оси х, у и z, как это делалось в п.1.2 для точки внутри тела, получим уравнения, в которых компоненты полного напряжения на наклонной площадке 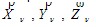 надо соответственно заменить на компоненты поверхностной нагрузки рх, ру, pz, а именно: надо соответственно заменить на компоненты поверхностной нагрузки рх, ру, pz, а именно:
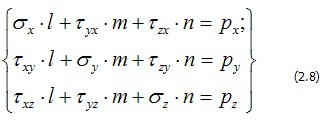
В сокращенной записи условия на поверхности (2.8) представим виде

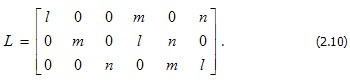
Далее -> |



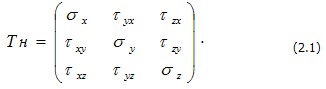

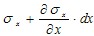 . С учетом сказанного на рис.2.1, б показаны все компоненты напряжений, параллельные оси х.
. С учетом сказанного на рис.2.1, б показаны все компоненты напряжений, параллельные оси х. 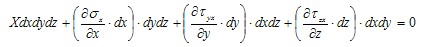

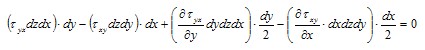
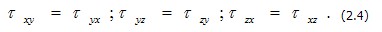
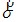 и вектор интенсивности объемной нагрузки
и вектор интенсивности объемной нагрузки 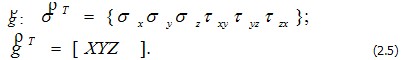


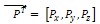 и напряжениями в произвольной точке поверхности тела. На рис. 2.2, а) показан элементарный тетраэдр, выделенный у поверхности тела сечениями, параллельными координатным плоскостям, и плоскостью, касательной к поверхности. Ориентацию последней определяет нормаль , направляющие косинусы которой обозначим:
и напряжениями в произвольной точке поверхности тела. На рис. 2.2, а) показан элементарный тетраэдр, выделенный у поверхности тела сечениями, параллельными координатным плоскостям, и плоскостью, касательной к поверхности. Ориентацию последней определяет нормаль , направляющие косинусы которой обозначим: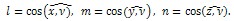

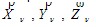 надо соответственно заменить на компоненты поверхностной нагрузки рх, ру, pz, а именно:
надо соответственно заменить на компоненты поверхностной нагрузки рх, ру, pz, а именно: