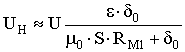ГЛАВНАЯ | МЕТОДИЧЕСКИЕ УКАЗАНИЯ | ОПИСАНИЕ КУРСА | ЛИТЕРАТУРА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
Основы расчета электромагнитных преобразователей
Электромагнитные преобразователи составляют основу обширной группы датчиков механических величин, нашедших широкое распространение при автоматизации производственных процессов.
Среди многообразия электромагнитных преобразователей выделим два основных типа: индуктивные и трансформаторные. Преобразователи, преобразующие входную величину, например, механическое перемещение, в изменение индуктивности, называются индуктивными. Преобразователи, преобразующие перемещение в изменение взаимоиндуктивности, принято называть трансформаторными, хотя более верное название – взаимоиндуктивные.
Одно из простых измерительных устройств с использованием преобразователя с изменяющейся индуктивностью показано на рис.1.
В данном устройстве измеряемая физическая величина осуществляет перемещение стального сердечника 2 относительно неподвижного магнитопровода 1. Указанное перемещение вызывает изменение индуктивности L катушки возбуждения, которое зависит от величины воздушного зазора ? или механического перемещения:
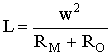 , (1)
, (1)
где 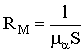 ;
; 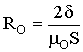 ;
;
RM – магнитное сопротивление магнитопровода;
RO – магнитное сопротивление воздушного зазора;
w – число витков;
S – площадь поперечного сечения магнитопровода.
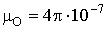 , Гн/м.
, Гн/м.
Формула (1) получена на основании закона Ома для магнитной цепи:
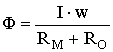
и известного выражения для потокосцепления ? и током I
?=wФ=LI.
Как следует из (1) L(дельта), то индуктивное сопротивление ХL=(омега)L тоже зависит от перемещения дельта. Изменение величины ? приводит к изменению тока в цепи (рис.1). Это следует из закона Ома для электрической цепи I=U/Z.
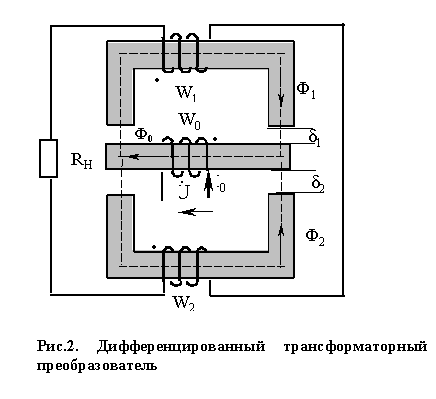
Принципиальная схема измерения линейных перемещений, вызываемых исследуемой физической величиной, с использованием трансформаторного преобразователя показана на рис. 2.
Обмотка возбуждения w0 преобразователя укреплена на среднем подвижном сердечнике. Изменение магнитного сопротивления отдельных участков магнитной цепи осуществляется при перемещении среднего сердечника за счет изменения воздушных зазоров ?1, ?2.
Изменения магнитных сопротивлений участков магнитной цепи определяет распределение магнитных потоков Ф1 и Ф2, сцепляющихся с измерительными обмотками w1, w2. Изменение потоков Ф1 и Ф2 приводит к изменению параметров обмоток, а также индуктированных в обмотках э.д.с.
Рассмотрим алгоритм решения подобных задач на примере преобразователя, приведенного на рис. 2.
Алгоритм расчета
- Изобразите комплексную схему замещения электрической цепи рассматриваемого преобразователя при наличии магнитно-связанных катушек.
- Выведите формулу для тока и напряжения нагрузки в измерительной обмотке преобразователя.
- Определите распределения магнитных потоков
а) составление расчетной магнитной цепи;
б) выбор направлений магнитных потоков и м.д.с.:
- направление магнитных потоков выбираем произвольно;
- направление МДС определяется по правилу правой руки;
в) выбор участков магнитной цепи из учета постоянства магнитной напряженности Н, определение их сечений и длин средних линий;
г) определение магнитных потоков, например, по законам Кирхгофа;
д) расчет параметров преобразователя: индуктивностей и взаимоиндуктивностей обмоток;
- С учётом известных коэффициентов LK, MLK рассчитайте напряжение в нагрузке согласно формулам п. 2.
Примечание:
При расчёте тока в измерительной обмотке преобразователя, согласно приведенному алгоритму, пренебрегаем потерями в стали, поверхностным эффектом, распором силовых линий магнитного поля у краёв воздушных зазоров. Последний эффект можно не учитывать, если максимальная длина воздушного зазора не превышает более, чем в 2-3 раза минимальный размер поперечного сечения магнитопровода. В этом случае алгоритм расчёта магнитной цепи переменного тока совпадает с расчётом магнитной цепи постоянного тока.
Расчёт преобразователя
Комплексная схема замещения магнитно-связанных катушек изображена на рис. 3.
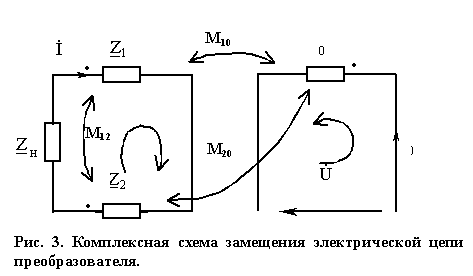
Поток одной из катушек пронизывает и наводит в них э.д.с. взаимоиндукции, которые должны быть учтены при расчёте через соответствующие коэффициенты взаимной индуктивности МLK. При составлении уравнений для магнитно-связанных цепей необходимо знать, согласно или встречно включены катушки.
Если на электрической схеме токи рассматриваемых катушек одинаково ориентированы относительно одноименных зажимов (например, начала катушек, которые на схеме обозначены точками), то имеет место согласованное включение, в противном случае – встречное.
Из магнитной схемы (рис. 2) или комплексной схемы замещения (рис. 3) видно, что катушки w0,w1 включены согласовано, а катушки w1, w2 и w0, w2 – встречно.
С учётом вышеизложенного из второго закона Кирхгофа запишем комплексную систему уравнений для токов:
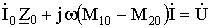 (2)
(2)
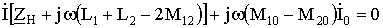
При записи комплексной системы (2) принебрегаем активным сопротивлением катушек и в дальнейшем будем считать, что 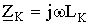 . Так как катушки W1 и W0 включены согласовано, перед слагаемым
. Так как катушки W1 и W0 включены согласовано, перед слагаемым 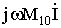 поставлен тот знак, что и перед
поставлен тот знак, что и перед 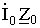 . А знак «+» перед слагаемым
. А знак «+» перед слагаемым 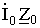 определён из второго закона Кирхгофа согласно указанному на рис. 3 направлению обхода контура. Знак «- » перед слагаемым
определён из второго закона Кирхгофа согласно указанному на рис. 3 направлению обхода контура. Знак «- » перед слагаемым 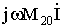 определяется встречным включением катушек w2 и w0.
определяется встречным включением катушек w2 и w0.
Из (2) определяем ток возбуждения 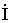 и напряжение на сопротивлении нагрузки
и напряжение на сопротивлении нагрузки 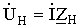
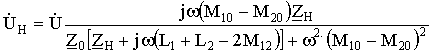 (3)
(3)
Из анализа формулы (3) видно, что напряжение 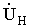 пропорционально разности М10 – М20 и зависит от сопротивления нагрузки
пропорционально разности М10 – М20 и зависит от сопротивления нагрузки 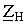 .
.
Для количественной оценки величины напряжений надо рассчитать магнитные параметры: LK, MLK. Для этого необходимо определить распределение магнитных потоков согласно вышеизложенного алгоритма.
Пренебрегая потоками рассеивания, исходя из законов Кирхгофа для магнитной цепи, получим:
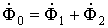 ;
;
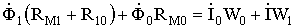 ; (4)
; (4)
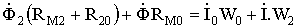 ;
;
где RM1, RM2 – магнитные сопротивления верхнего и нижнего сердечников магнитной цепи преобразователя;
RMO – магнитное сопротивление среднего подвижного сердечника;
R10, R20 –магнитные сопротивления воздушных зазоров ?1, ?2, соответственно.
Решение системы (4) для потокосцеплений ?к, которые связаны с исследуемыми Фк магнитными потоками
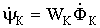 (к=0, 1, 2)
(к=0, 1, 2)
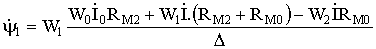
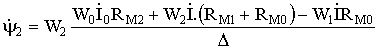 (5)
(5)
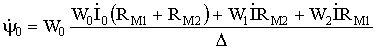
где RM1, RM2 – полные магнитные сопротивления верхнего и нижнего сердечников, равные сумме Rмi+ Rio соответственно.
Знаменатель ? в (5) равен
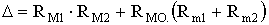 .
.
Учитывая, что индуктивность катушек LK пропорциональна квадрату числа их витков w2K, а коэффициент взаимной индуктивности МLK между L и K катушек пропорционален произведению витков w1wk, опре-делим параметры обмоток трансформаторного преобразователя из анализа выражений (5).
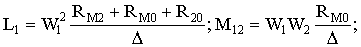
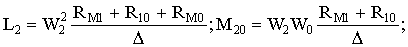 (6)
(6)
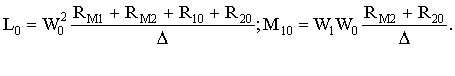
Магнитные сопротивления всех участков рассматриваемого преобразователя можно рассчитать, зная геометрические размеры, площади сечения магнитопровода и марку стали, и ограничиваясь прямолинейным участком кривой намагничивания. Тогда согласно (6) можно рассчитать параметры LK, MLK и из (3) найти выражение UH в нагрузке.
В заключении необходимо отметить,что разность М10-М20 прямо пропорциональна разности воздушных зазоров ?1- ?2 . Тогда из (3):
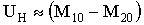 .
.
Рабочие воздушные зазоры преобразователя выразим через начальные зазоры ?0, их приращение – через ?:
?1= ?0(1+ ?); ?2= ?0(1- ?).
Тогда результирующее напряжение
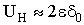 . (7)
. (7)
Из (7) следует, что в исходном состоянии ?=0 напряжение в нагрузке отсутствует, а при перемещении сердечника на величину ??0 сигнал пропорционален 2 ??0 . При работе преобразователя близкому к х.х. 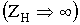 и при условии W1=W2=W0 формула (3) упрощается и принимает вид
и при условии W1=W2=W0 формула (3) упрощается и принимает вид
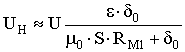
ГЛАВНАЯ | МЕТОДИЧЕСКИЕ УКАЗАНИЯ | ОПИСАНИЕ КУРСА | ЛИТЕРАТУРА
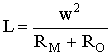 , (1)
, (1)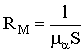 ;
; 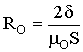 ;
;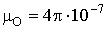 , Гн/м.
, Гн/м.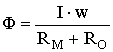


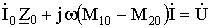 (2)
(2)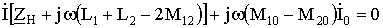
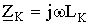 . Так как катушки W1 и W0 включены согласовано, перед слагаемым
. Так как катушки W1 и W0 включены согласовано, перед слагаемым 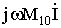 поставлен тот знак, что и перед
поставлен тот знак, что и перед 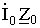 . А знак «+» перед слагаемым
. А знак «+» перед слагаемым 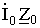 определён из второго закона Кирхгофа согласно указанному на рис. 3 направлению обхода контура. Знак «- » перед слагаемым
определён из второго закона Кирхгофа согласно указанному на рис. 3 направлению обхода контура. Знак «- » перед слагаемым 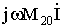 определяется встречным включением катушек w2 и w0.
определяется встречным включением катушек w2 и w0. 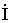 и напряжение на сопротивлении нагрузки
и напряжение на сопротивлении нагрузки 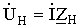
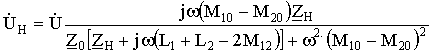 (3)
(3)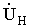 пропорционально разности М10 – М20 и зависит от сопротивления нагрузки
пропорционально разности М10 – М20 и зависит от сопротивления нагрузки 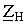 .
.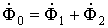 ;
;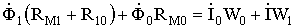 ; (4)
; (4)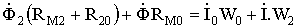 ;
;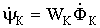 (к=0, 1, 2)
(к=0, 1, 2)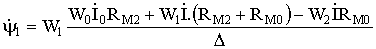
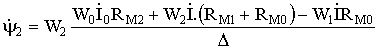 (5)
(5)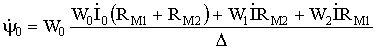
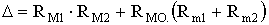 .
.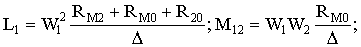
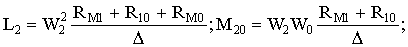 (6)
(6) 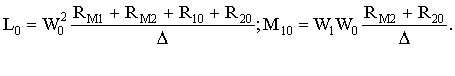
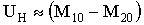 .
.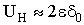 . (7)
. (7)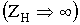 и при условии W1=W2=W0 формула (3) упрощается и принимает вид
и при условии W1=W2=W0 формула (3) упрощается и принимает вид