R1=R2=(М+1)кОм;
R3=R4=(11-М)кОм;
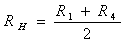
Например, при М=5
R1=R2=6кОм; R3=R4=6кОм; RН=6кОм.
ГЛАВНАЯ | МЕТОДИЧЕСКИЕ УКАЗАНИЯ | ОПИСАНИЕ КУРСА | ЛИТЕРАТУРА
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
ЦЕЛЬ РАБОТЫ
- электрических цепей с неравновесными мостами;
- неоднородных магнитных цепей.
СОДЕРЖАНИЕ МЕТОДИЧЕСКИХ УКАЗАНИЙ
АЛГОРИТМ РАСЧЕТА НЕРАВНОВЕСНОЙ МОСТОВОЙ ЦЕПИ ПОСТОЯННОГО ТОКА.
Исходные данные:
В представленной на рис. 1 мостовой схеме в состоянии равновесия сопротивления имеют следующие численные значения:
R1=R2=(М+1)кОм;
R3=R4=(11-М)кОм;
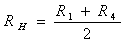
Например, при М=5
R1=R2=6кОм; R3=R4=6кОм; RН=6кОм.
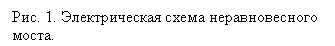
Предположим, что рабочими плечами, изменяющими свое сопротивление под действием измеряемой неэлектрической величины, являются R1 и R3.
Относительные изменения сопротивлений рабочих плеч:
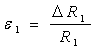 и
и 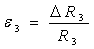
имеют по модулю одинаковую величину
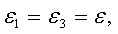
а по знаку R1 изменятся пропорционально (1+e), а R3 – пропорционально
(1-e).
Напряжение U=1В.
3.1. Расчет функций преобразования [4].
Функция преобразования – это зависимость напряжения на измерительной диагонали моста CD от изменений сопротивлений рабочих плеч, т.е.
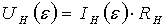
IН(e) рекомендуется определить методом эквивалентного генератора, согласно которому [1,2]
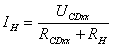 , (1)
, (1)
где UCDхх – напряжение между точками С и D для случая, когда RН отключено (рис.2);
RCDхх?к.з. всех Еi –RCD при отключенной нагрузке RН и при коротком замыкании всех источников напряжения (рис.3).
3.1.1. Определяем UCDхх.
При холостом ходе (RН - отключено) схема моста примет вид (рис.2).
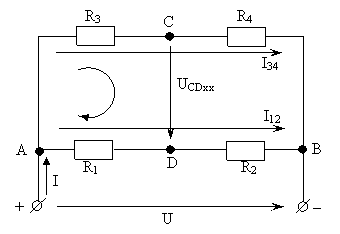
3.1.2. Находим RCDхх ?к.з. всех Еi.
В соответствии со схемой (рис.3)
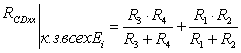 (3)
(3)
Подставив выражения (2) и (3) в уравнение (1), найдем
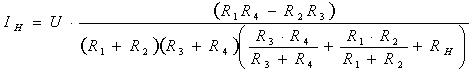
Тогда
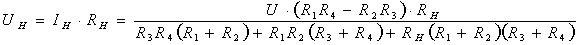 (4)
(4)
В выражение (4) подставим значения сопротивлений рабочих плеч, выраженные в зависимости от e: R1(1+e1) и R3(1-e3). Тогда получим
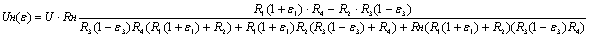 (5)
(5)
Подставив численные значения R1, R2, R3, R4 в (5), найдем
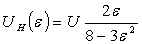 (6)
(6)
3.1.3. Расчет численных значений функции преобразования и построение ее графика
Задавая e в пределах -1?e?1 с шагом 0,1, рассчитываем значения UН(e) по формуле (6).
Результаты расчета сводим в таблицу.
Функция преобразования мостовой схемы
| e | -1,0 |
-0,9 |
-0,8 |
-0,7 |
-0,6 |
-0,5 |
-0,4 |
-0,3 |
-0,2 |
-0,1 |
0 |
UН |
-0,4 |
-0,3212 |
-0,2631 |
-0,2145 |
-0,1799 |
-0,1378 |
-0,1064 |
-0,0776 |
-0,0509 |
-0,0251 |
0 |
e |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1,0 |
|
UН |
0,0251 |
0,0509 |
0,0776 |
0,1064 |
0,1378 |
0,1799 |
0,2145 |
0,2631 |
0,3212 |
0 |
|
По полученным значениям строим график зависимости UН(e)
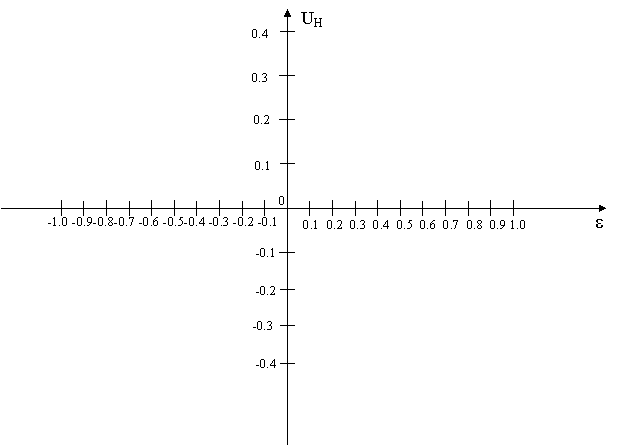
Из графика видно, что зависимость UН(e) линейна в интервале
-0,4<e<0,4.
3.2. Вывод условия равновесия моста [4]
Мост находится в равновесии, если UН=0 и IН=0, т.е.
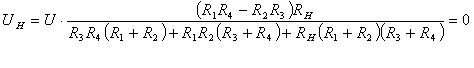
Дробь равна 0, если числитель равен 0 или знаменатель равен бесконечности. Знаменатель не равен бесконечности, т.к. заданы конечные значения сопротивлений R1, R2, R3, R4.
Следовательно, R1R4-R2R3=0 или
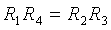 - это и есть условие равновесия моста:
- это и есть условие равновесия моста:
произведения сопротивлений противолежащих плеч моста должны быть равны.
3.3. Определение знака e рабочих плеч моста для получения максимальной величины UН
По условию изменяются сопротивления рабочих плеч моста R1 и R3.
3.3.1. Если задать приращения сопротивлений рабочих плеч одного знака, т.е. R1(1+e) и R3(1+e), то условие разбаланса моста примет вид:
R1(1+e)R4-R2R3(1+e)=R1R4+e R1R4- R2R3-e R2R3=0
Т.к. R1=R2 и R3=R4 (по условию), то получим 0=0, т.е. нет разбаланса.
3.3.2. Если R1(1+e), а R3(1-e), то условие разбаланса примет следующий вид:
R1(1+e)R4-R2R3(1-e)=R1R4+e R1R4- R2R3+e R2R3=2eR1R4-
это и будет определять максимальный разбаланс моста.
Следовательно, если рабочие плечи – R1 и R3, т.е. противолежащие в мосте, то для получения максимального значения UН необходимо, чтобы приращения сопротивлений R1 и R3 были с противоположными знаками.
3.4. Определение нелинейности моста
3.4.1. Вывод формулы нелинейности моста при RН
Под нелинейностью функции преобразования принимают выражение:
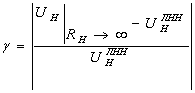 , (7)
, (7)
где 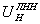 - линейная функция преобразования.
- линейная функция преобразования.
Из выражения (2) следует, что
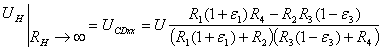
После преобразования приведенного выражения и введения коэффициента симметрии моста
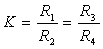
получится
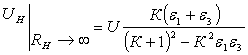 (8)
(8)
Для получения 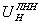 необходимо в знаменателе пренебречь слагаемыми, содержащими e, а в числителе слагаемыми, содержащими степени e. Тогда:
необходимо в знаменателе пренебречь слагаемыми, содержащими e, а в числителе слагаемыми, содержащими степени e. Тогда:
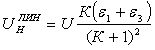 (9)
(9)
Подставим (8) и (9) в выражение (7) для g.
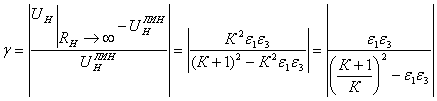 (10)
(10)
3.4.2. Определение знака e для получения минимальной нелинейности моста
Определим знак e для получения gmin, для чего рассчитаем g при e=0,5 и e=-0,5. Если 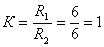 (по условию) и ?e1?=?e3?=e, то
(по условию) и ?e1?=?e3?=e, то
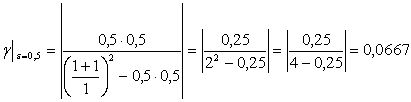 ;
;
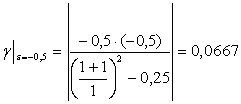 ,
,
т.е. в данном случае нелинейность одинакова при e=±0,5.
3.4.3. Расчет коэффициента нелинейности при e=0,2
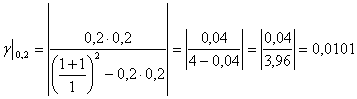
3.5. Определение величины К, обеспечивающей максимальную чувствительность моста (для вариантов N=6?9).
Чувствительность моста S-это отношение приращения выходной величины к вызвавшему его приращению входной величины.
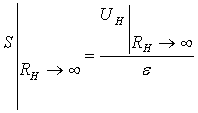 (11)
(11)
Известно, что S=max, если 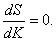
Определив 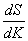 по выражению(11) и приравняв его 0, получим численное значение К, соответствующее Smax.
по выражению(11) и приравняв его 0, получим численное значение К, соответствующее Smax.
ГЛАВНАЯ | МЕТОДИЧЕСКИЕ УКАЗАНИЯ | ОПИСАНИЕ КУРСА | ЛИТЕРАТУРА