8.4. Синтез систем автоматического управления
Синтез системы управления представляет собой направленный расчет системы, имеющий конечной целью, во-первых, отыскание рациональной структуры системы и, во-вторых, определение оптимальных значений параметров ее отдельных звеньев из условия обеспечения ряда требований, которые следуют из назначения проектируемой системы и обеспечения ее характеристик.
Синтез можно трактовать как задачу оптимизации и рассматривать такое построение системы управления, при котором для заданных условий работы обеспечивается оптимум выбранного критерия качества работы системы.
Если характеристики задающих и возмущающих воздействий известны, то систему можно спроектировать как оптимальную, обеспечив минимальное значение суммарной среднеквадратической ошибки. Решить эту задачу позволяет теория оптимальных фильтров Н.Винера и Р.Калмана.
Наиболее общей является постановка задачи достижения минимума функционала
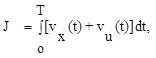 (8.10)
(8.10)
где vx(t) - квадратичная форма относительно ошибки системы;
vu(t) - квадратичная форма относительно управляющего воздействия;
T - время работы системы.
Первая квадратичная форма в (8.10) выбирается из требований к точности проектируемой системы, а вторая учитывает ограничения на управляющее воздействие u(t). При этом из допустимого множества u(t) необходимо выбрать и технически реализовать такое управляющее воздействие, которое переводит объект управления из начального состояния в конечное и минимизирует функционал (8.10). Для решения таких задач используются методы вариационного исчисления, принцип максимума Л.С.Понтрягина, метод динамического программирования Р.Белмана. Здесь возможны два случая, во-первых, полностью известна информация о состоянии объекта управления, во-вторых, информация об объекте управления неполная или вообще неизвестна. Во втором случае при синтезе системы возникает дополнительная задача оценки состояния объекта управления, на основании которой формируется оптимальное управляющее воздействие.
Синтез можно трактовать как инженерную задачу, сводящуюся к такому построению системы управления, при котором обеспечивается выполнение технических требований к ней. Один из возможных способов описания требований к проектируемой системе - задание показателей качества работы системы, рассмотренных в разделе 6. Это может быть сделано, если известны характеристики задающих и возмущающих воздействий. Детерминированные воздействия должны быть заданы как функции времени или их производные. Для случайных воздействий должны быть известны их корреляционные функции или спектральные плотности. При такой постановке синтез системы сводится к выбору структурной схемы, с помощью которой можно обеспечить показатели качества работы системы не хуже заданных.
Иногда в понятие инженерного синтеза вкладывается еще более узкий смысл и рассматривается синтез, имеющий целью определение вида и параметров корректирующих средств, которые необходимо добавить к неизменной части системы - объекту управления с регулятором, чтобы обеспечить требуемые динамические качества. Обеспечение необходимого качества управления достигается выработкой вполне определенного закона управления u(t). Для этого необходимо, чтобы при известной передаточной функции объекта управления WОУ(s) регулятор имел определенную передаточную функцию WR(s) и, соответственно, передаточная функция разомкнутой системы должна быть W(s) = WR(s)WОУ(s).
При инженерном синтезе системы управления необходимо обеспечить, во-первых, требуемую точность, во-вторых, приемлемый характер переходных процессов.
Частотный метод синтеза корректирующих устройств. Наиболее распространен частотный метод синтеза с помощью логарифмических частотных характеристик. Логарифмическая амплитудная частотная характеристика разомкнутой системы управления однозначно определяется ее передаточной функцией и соответственно наоборот, логарифмической амплитудной частотной характеристике однозначно соответствует передаточная функция разомкнутой системы. Следовательно, на основе требований, предъявляемых к системе можно сформировать желаемый вид ЛАХ, которой будет соответствовать требуемая передаточная функция системы и закон управления. На основе этой взаимосвязи и построен метод синтеза систем автоматического управления по логарифмическим частотным характеристикам.
Процесс синтеза системы управления включает в себя следующие пункты.
1. Построение располагаемой ЛАХ LР(ω). Под располагаемой ЛАХ понимается характеристика исходной системы, состоящей из объекта управления и регулятора и не снабженной корректирующими средствами, обеспечивающими требуемое качество работы. Располагаемая ЛАХ LР(ω) строится по виду располагаемой передаточной функции WР(s) исходной разомкнутой системы.
Замечание: при построении располагаемой ЛАХ обычно значение общего коэффициента передачи разомкнутой системы koбщ выбирается на основании требований, предъявляемых к точности системы управления (см. п.2).
2. Построение желаемой ЛАХ Lж(ω). Желаемая логарифмическая амплитудная частотная характеристика формируется исходя из заданных требований к системе по точности и качеству переходного процесса. Точность задается значениями установившихся ошибок, а качество переходного процесса - величиной перерегулирования и временем регулирования.
Построение желаемой ЛАХ производится по частям.
Низкочастотная часть желаемой ЛАХ формируется из условия обеспечения требуемой точности работы системы управления в установившемся режиме, то есть из условия того, что установившаяся ошибка системы x(∞) не должна превышать заданное значение Δ3 (x(∞) ≤Δ3).
Требования точности системы формулируются по разному. В системах управления величина установившейся ошибки зависит от общего коэффициента передачи разомкнутой системы и вида задающего воздействия.
Для систем стабилизации при постоянном задающем воздействии g(t)=g0=const установившаяся ошибка xg(∞) = g0/(1+ koбщ).
Откуда желаемое значение общего коэффициента передачи разомкнутой системы
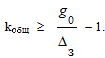 (8.11)
(8.11)
Таким образом, низкочастотная часть желаемой ЛАХ должна иметь наклон 0 дб/дек и проходить не ниже точки с координатами: ω=1 c-1, L(1)=20lg koбщ [дб].
Если требуется обеспечить слежение за задающим воздействием g(t)=g1t при g1=const, то установившаяся ошибка xg(∞) = g1/koбщ .
Отсюда находим желаемое значение
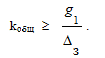 (8.12)
(8.12)
Таким образом, низкочастотная часть желаемой ЛАХ должна иметь наклон -20 дб/дек и проходить не ниже точки с координатами: ω=1 c-1, L(1)=20lg koбщ [дб].
При отработке гармонического задающего воздействия g(t)=gmsinωkt точность оценивается по величине амплитуды ошибки, вычисляемой по выражению (6.15).
В этом случае модуль желаемой частотной передаточной функции разомкнутой системы на частоте качки ωk должен удовлетворять условию
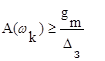 (8.13)
(8.13)
Таким образом, низкочастотная часть желаемой ЛАХ должна иметь наклон -20 дб/дек и проходить не ниже точки AК (рис.8.6) с координатами: ωk [c-1], LK=L(ωk) = 20lgA(ωk ) [дб].
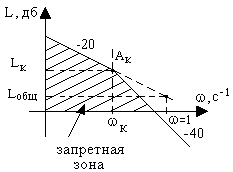
Рис. 8.6. Запретная область для желаемой ЛАХ
Для определения общего коэффициента передачи разомкнутой системы koбщ по низкочастотной части желаемой ЛАХ находят амплитуду Lобщ на частоте ω=1 с-1, тогда
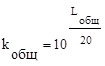 (8.14)
(8.14)
Часто точный закон изменения задающего воздействия неизвестен, а заданы только максимальная скорость и максимальное ускорение задающего воздействия. В этом случае при расчете используют эквивалентное гармоническое воздействие, наибольшее значение первой производной которого равно заданному максимальному значению скорости, а наибольшее значение второй производной - максимальному значению ускорения. Тогда частота качки ωk и амплитуда эквивалентного гармонического воздействия определяются по формулам:
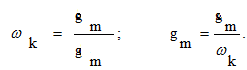 (8.15)
(8.15)
Если скорость задающего воздействия максимальная, а ускорение убывает, то точка AК (рис.8.6) будет двигаться по прямой с наклоном -20дб/дек в диапазоне частот ω<ωk. Если же ускорение равно максимальному, а скорость убывает, то точка AК двигается по прямой с наклоном -40дб/дек в диапазоне частот ω>ωk. Область, расположенная ниже точки AК и двух прямых с наклоном -20дб/дек и -40дб/дек, представляет собой запретную область для желаемой логарифмической амплитудной частотной характеристики системы.
Среднечастотный участок желаемой ЛАХ строится из условия обеспечения основных показателей качества переходного процесса - перерегулирования и времени регулирования. Это достигается тем, что среднечастотный участок желаемой ЛАХ (рис.8.8) имеет наклон -20 дб/дек (см. раздел 5.6) и пересекает ось частот на частоте среза ωс, которая определяется по номограмме В.В.Солодовникова (см. раздел 6.4), исходя из заданных значений величины перерегулирования σ и времени регулирования tр.
а)
б)
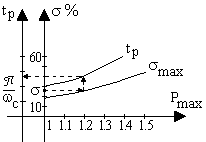
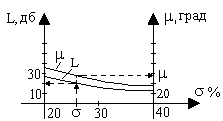
Рис. 8.7. Номограммы В.В.Солодовникова
По номограмме (рис.8.7,а), отложив заданную величину σ (например, 25%), определяем величину tр (как показано стрелками), например,
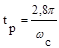
Поскольку требуемое значение tр задается, можно вычислить необходимую частоту среза
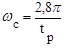 (8.16)
(8.16)
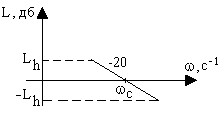
Рис. 8.8. Среднечастотный участок желаемой ЛАХ
Протяженность среднечастотного участка определяется номограммой (рис.8.7,б), устанавливающей связь между показателями качества и запасами устойчивости. Так, например, для обеспечения σ=25% требуется запас устойчивости по модулю Lh=20 дб и по фазе μ=580. Среднечастотный участок проводится с наклоном -20 дб/дек влево и вправо от частоты среза ωс до достижения модулей, равных Lh и -Lh. После этого участки средних и низких частот сопрягаются прямой с наклоном -40 или -60 дб/дек, как удобнее.
Высокочастотный участок желаемой ЛАХ проводится параллельно высокочастотному участку располагаемой ЛАХ. Область высоких частот содержит те сопрягающие частоты, пренебрежение которыми не изменяет существенного вида ЛЧХ системы в области средних частот. Можно считать, что “малыми” параметрами, не влияющими существенно на динамику системы, являются постоянные времени, удовлетворяющие условиям
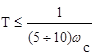 (8.17)
(8.17)
3. Определение передаточных функций Wж(s) желаемой разомкнутой системы и Фж(s) желаемой замкнутой системы. Желаемая передаточная функция разомкнутой системы Wж(s) находится по виду желаемой ЛАХ Lж(ω), а желаемая передаточная функция замкнутой системы Фж(s) определяется по методике, изложенной в разделе 4.1. Затем строятся фазовая частотная характеристика желаемой разомкнутой системы и переходная характеристика желаемой замкнутой системы и оцениваются фактически получающиеся величины запасов устойчивости и качественные показатели системы. Если полученные при этом показатели качества не превышают требуемых значений, определенных заданием, то построение желаемой ЛАХ считается законченным, иначе построенную желаемую ЛАХ необходимо скорректировать.
Если получившаяся величина перерегулирования превышает заданное значение, то требуется расширение среднечастотного участка желаемой ЛАХ.
Если время регулирования получается больше заданного, то необходимо увеличить частоту среза.
На рис.8.9, в качестве примера, приведены ЛАХ располагаемой Lр(ω) и ЛАХ желаемой Lж(ω) разомкнутой системы.
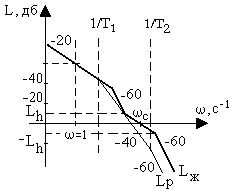
Рис. 8.9. ЛАХ располагаемой и желаемой разомкнутой системы
Здесь располагаемая передаточная функция разомкнутой системы
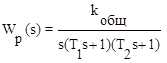 (8.18)
(8.18)
и желаемая
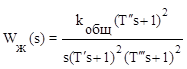 (8.19)
(8.19)
где koбщ=1000 с-1.
4. Определение вида и параметров корректирующего устройства.
Расчет последовательных корректирующих устройств.
В случае выбора последовательного корректирующего устройства желаемая передаточная функция разомкнутой системы имеет вид
Wж(s)=WПКУ(s)Wp(s) (8.20)
где WПКУ(s) - передаточная функция последовательного корректирующего устройства;
Wр(s) - передаточная функция располагаемой системы.
Тогда логарифмическая амплитудная частотная характеристика желаемой системы
Lж(ω) = Lр(ω) + LПКУ(ω). (8.21)
Следовательно, логарифмическая амплитудная частотная характеристика последовательного корректирующего устройства
LПКУ(ω) = Lж(ω) - Lр(ω). (8.22)
Выражение (8.22) показывает, что для определения последовательного корректирующего устройства необходимо:
а) по располагаемой передаточной функции Wр(s) построить ЛАХ располагаемой системы Lр(ω);
б) по заданным показателям качества построить ЛАХ желаемой системы Lж(ω);
в) вычесть из желаемой ЛАХ располагаемую ЛАХ, что позволит найти требуемую ЛАХ последовательного корректирующего устройства LПКУ(ω);
г) по виду ЛАХ последовательного корректирующего устройства LПКУ(ω) определить его передаточную функцию WПКУ(s) и схему.
На рис.8.10, в качестве примера, представлены ЛАХ располагаемой Lр(ω), ЛАХ желаемой Lж(ω) разомкнутой системы и ЛАХ последовательного корректирующего устройства LПКУ(ω).
В результате получаем
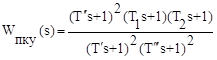
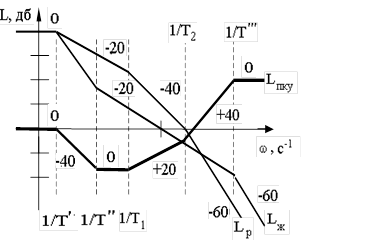
Рис.8.10. ЛАХ располагаемой и желаемой разомкнутой системы и последовательного корректирующего устройства
Расчет корректирующих обратных связей.
В случае выбора корректирующего устройства типа обратной связи желаемая передаточная функция разомкнутой системы имеет вид
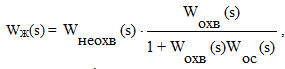 (8.23)
(8.23)
где WНЕОХВ(s) - передаточная функция звеньев располагаемой системы, неохваченных обратной связью;
WОХВ(s) - передаточная функция звеньев располагаемой системы, охватываемых обратной связью;
WОС(s) - передаточная функция корректирующей обратной связи.
Выбор обратных связей выполняется для тех диапазонов частот, для которых справедливо неравенство
|WОХВ(jω) WОС(jω)|>>1. (8.24)
В этом случае логарифмическая амплитудная частотная характеристика желаемой системы будет
LЖ(ω) = LНЕОХВ(?ω) -LОС(ω). (8.25)
Следовательно, логарифмическая амплитудная частотная характеристика корректирующей обратной связи
LОС(ω) = LНЕОХВ(ω) - LЖ(ω). (8.26)
Выражение (8.26) показывает, что для определения корректирующей обратной связи необходимо:
а) по передаточной функции WНЕОХВ(s) звеньев располагаемой системы, не охваченных обратной связью, построить ЛАХ неохваченных звеньев LНЕОХВ(ω);
б) по заданным показателям качества построить ЛАХ желаемой системы LЖ(ω);
в) вычесть из ЛАХ неохваченных звеньев LНЕОХВ(ω) желаемую ЛАХ LЖ(ω), что позволит найти требуемую ЛАХ корректирующей обратной связи LОС(ω);
г) по виду ЛАХ корректирующей обратной связи LОС(ω) определить ее передаточную функцию WОС(s) и схему.
В случае необходимости последовательное корректирующее устройство или корректирующая обратная связь могут быть пересчитаны на эквивалентное параллельное корректирующее звено согласно выражению (8.9).
5. Техническая реализация корректирующих средств. По полученной передаточной функции необходимо создать реальное корректирующее устройство, которое реализуется аппаратно или программно. В случае аппаратной реализации требуется подобрать схему и параметры корректирующего звена. В литературе [7,10,12] имеются таблицы типовых корректирующих устройств как пассивных, так и активных.
На рис.8.11 приведена блок-схема алгоритма синтеза систем управления.
ЦДО ДГТУ © 2012


