7.2. Теория инвариантности и комбинированное управление
Одним из эффективных способов, позволяющих получить высокую точность в системах управления, является использование методов теории инвариантности. Система управления является инвариантной по отношению к внешним воздействиям, если после завершения переходного процесса, определяемого начальными условиями, ошибка системы не зависит от внешних воздействий.
Основной принцип управления состоит в формировании управляющего воздействия по величине ошибки. Если же вводятся компенсирующие цепи по внешним воздействиям, то получается комбинированное управление - по ошибке и по внешним воздействиям.
При введении компенсаций по внешним воздействиям теоретически при определенных условиях удается сводить величину ошибки к нулю для любых внешних воздействий. Это свойство инвариантности системы по отношению к внешним воздействиям.
Внешние воздействия делятся на задающие, которые система должна воспроизводить, и возмущающие, действие которых требуется нейтрализовать.
Комбинированная система по задающему воздействию. Здесь, наряду с отклонением, во внутреннюю цепь системы вводится сигнал от задающего воздействия с помощью компенсирующего устройства по задающему воздействию с передаточной функцией WКЗ(s) (рис.7.3).
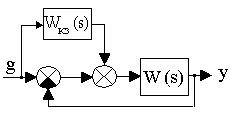
Рис. 7.3. Структурная схема комбинированной системы по задающему воздействию
Эквивалентная передаточная функция замкнутой системы с учетом управления по задающему воздействию будет равняться
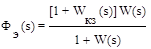 . (7.4)
. (7.4)
а для ошибки -
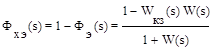 . (7.5)
. (7.5)
Установившаяся ошибка будет равняться нулю для любого задающего воздействия при ФХЭ(S)=0, то есть если
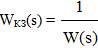 . (7.6)
. (7.6)
Разложив последнее выражение в ряд по возрастающим степеням оператора s, получим необходимый вид функции, определяющей компенсирующий сигнал от задающего воздействия:
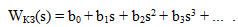 . (7.7)
. (7.7)
Таким образом, в комбинированной системе по задающему воздействию для получения полной инвариантности необходимо вводить первую и высшие производные от задающего воздействия.
Полностью инвариантную систему реализовать сложно, но всегда можно сделать систему инвариантную до ε, где ε - допустимая ошибка работы системы.
Комбинированная система по возмущающему воздействию. В этом случае наряду с управлением по отклонению используется управление по возмущающему воздействию f(t). Передаточная функция компенсирующего устройства по возмущающему воздействию WКВ(s) для системы инвариантной к возмущающему воздействию определяется аналогично рассмотренному выше случаю.
Передаточная функция замкнутой системы для управляемой величины по возмущающему воздействию имеет вид [1]:
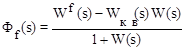 . (7.8)
. (7.8)
где W(s) - передаточная функция разомкнутой системы;
Wf(s) - передаточная функция по возмущающему воздействию в разомкнутой системе.
Условие полной инвариантности может быть получено, если положить Фf(s)=0.
Тогда
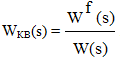 . (7.9)
. (7.9)
Эта функция может быть представлена в виде ряда, аналогично (7.7). Здесь также можно ограничиться неполной инвариантностью, если точное удовлетворение условию (7.9) вызывает технические трудности.
Особая трудность заключается в том, что возмущающие воздействия f(t), в отличие от задающих g(t), далеко не всегда можно подать на входы компенсирующих цепей.
Положительной особенностью комбинированных систем является то, что введение компенсирующих устройств по внешним воздействиям, как следует из выражений для передаточных функций (7.4) и (7.8), не меняет характеристическое уравнения системы, работающей по отклонению. Это означает, что не будут нарушаться не только условия устойчивости, но сохраняются и оценки качества переходного процесса.
Следовательно, этот способ существенно повышает точность системы без заметного ухудшения качества переходного процесса.
ЦДО ДГТУ © 2012


