6.7. Моделирование систем управления
Моделирование систем управления - это эффективный инструмент исследования сложных систем.
Модель представляет собой изображение оригинала на основе принятых гипотез и аналогий, а моделирование - представление объекта моделью для получения информации об этом объекте путем проведения экспериментов с его моделью.
Основное требование, которому должна удовлетворять модель, является ее адекватность объекту. Адекватность зависит от цели моделирования и принятых критериев. Модель адекватна объекту, если результаты моделирования подтверждаются на практике и могут служить основой для прогнозирования процессов, протекающих в исследуемых объектах.
Моделирование решает задачи изучения и исследования объектов, предсказания их функционирования, синтеза структуры, параметров и алгоритмов поведения.
Модели бывают математические и физические. Физические модели сохраняют физические свойства объекта, а математические модели представляют собой математические конструкции. В основе математического моделирования лежит подобие дифференциальных уравнений, которыми описываются процессы, происходящие в реальной системе и в модели. В настоящее время универсальным инструментом реализации математических моделей является ЭВМ. Цифровое моделирование систем управления основывается на численном решении уравнений, описывающих систему.
Рассмотрим систему с одним входом g(t) и одним выходом y(t). Передаточная функция замкнутой системы в общем случае имеет вид
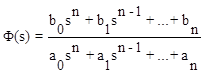 . (6.31)
. (6.31)
где n - порядок системы.
Если порядок числителя передаточной функции (6.31) окажется меньше порядка знаменателя, т.е. m
Передаточной функции замкнутой системы соответствует дифференциальное уравнение
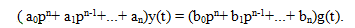 . (6.32)
. (6.32)
Для получения обобщенной модели системы это уравнение разрешают относительно старшей производной выходной величины:
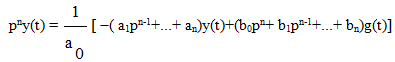 . (6.33)
. (6.33)
или
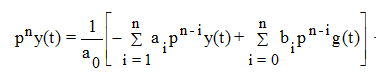 . (6.34)
. (6.34)
Таким образом, чтобы найти выходную величину y(t) необходимо pny(t) проинтегрировать n раз.
Уравнению (6.34) соответствует структурная схема модели, представленная на рис.6.8.
Для программной реализации полученной схемы решения исходного дифференциального уравнения (6.32) последнее переписывают в форме Коши. Для этого вводятся промежуточные переменные x1, ... , xn, соответствующие выходным величинам интеграторов. В результате получим следующую систему уравнений:
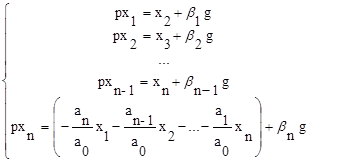 . (6.35)
. (6.35)
и уравнение связи
y(t) = x1 + β0g(t). (6.36)
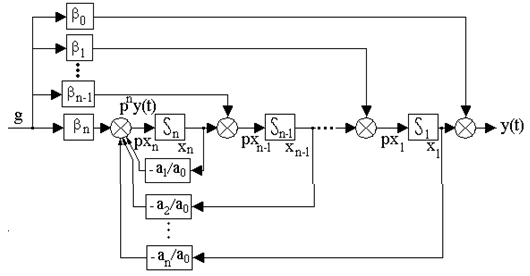
Рис. 6.8. Структурная схема модели системы
Коэффициенты βi (где i=0, 1, 2, ... , n) определяются из условия эквивалентности системы уравнений (6.35), (6.36) исходному дифференциальному уравнению (6.32) и вычисляются последовательно следующим образом:
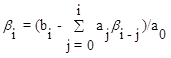 . (6.37)
. (6.37)
В настоящее время разработано большое количество систем моделирования, например, Continuous System Simulation Environment (CSSE).
ЦДО ДГТУ © 2012


