6.4. Частотные оценки качества
В инженерной практике для оценки показателей качества и построения переходных процессов в системах автоматического управления получили распространение частотные методы, разработанные В.В.Солодовниковым [7].
Математической основой частотных методов, устанавливающих связь между частотными характеристиками системы и качеством переходного процесса, является обратное преобразование Лапласа. Как известно, переходный процесс в системе определяется по формуле обратного преобразования Лапласа:
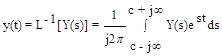 . (6.20)
. (6.20)
Установлено, что если на систему действует единичное задающее воздействие, т.е. g(t)=1(t), а начальные условия являются нулевыми, то реакцию системы, которая представляет собой переходную характеристику, в этом случае можно определить как
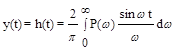 . (6.21)
. (6.21)
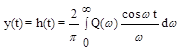 . (6.22)
. (6.22)
где P(ω) - вещественная частотная характеристика замкнутой системы;
Q(ω) - мнимая частотная характеристика замкнутой системы, т.е.
Фg(jω) = P(ω)+jQ(ω).
Выражения (6.21) и (6.22) и используются для оценок качества переходного процесса. Существует приближенный способ построения кривой переходного процесса в замкнутой системе по этим формулам с использованием h-функций.
Простейшими из частотных оценок качества переходного процесса являются запасы устойчивости, рассмотренные в разделе 5.5. Они определяют только степень близости замкнутой системы к границе устойчивости по виду частотных характеристик разомкнутой цепи.
Время регулирования и перерегулирование можно приблизительно оценить по виду вещественной частотной характеристики замкнутой системы (Рис.6.3). На основании зависимости (6.21) выведены следующие оценки. В переходном процессе получится перерегулирование σ>18%, если P(ω) имеет “горб”. При отсутствии “горба” будет σ<18%. Процесс окажется наверняка монотонным (σ=0), если dP/dω<0 и монотонно убывает по абсолютному значению. Время регулирования tр оценивается приблизительно по величине интервала существенных частот ωсу, причем
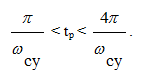 . (6.23)
. (6.23)
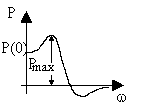
Рис.6.3. Вещественная частотная характеристика замкнутой системы
Интервал частот 0≤ω≤ωп, в котором P(ω)≥0, называется интервалом положительности. Интервал частот 0≤ω≤ωωсу называется интервалом существенных частот, если при ω=ωсу и далее при ω>ωсу величина |P(ω)| становится и остается меньше 0,05P(0). Влиянием остальной части вещественной частотной характеристики (при ω≥ωсу) на качество переходного процесса можно пренебречь. Если же при ω>ωп оказывается, что |P(ω)|<0,2P(0), то при оценке качества переходного процесса можно принимать во внимание только интервал положительности 0≤ω≤ωп.
Важно отметить, что время tр обратно пропорционально величине ωсу, т.е. чем более растянута частотная характеристика, тем короче переходный процесс. Физически это связано с тем, что чем более высокие частоты “пропускает” система, тем она менее инерционна в своих реакциях на внешние воздействия.
Это же свойство позволяет связать время tр с частотой среза ωс частотной характеристики разомкнутой системы. Длительность переходного процесса tр тем меньше, чем больше частота среза ωс.
На основании расчетов переходных процессов по (6.21) В.В.Солодовников предложил оценивать величину перерегулирова-ния σ% и время регулирования tр в зависимости от величины максимума вещественной частотная характеристика замкнутой системы Pmax, построив для этой цели номограммы (рис.6.4).
Кроме того, свойство частотных характеристик таково, что начальная их часть влияет в основном на очертание конца переходного процесса y(t), причем P(0)=y(∞). Основное же влияние на качество переходного процесса оказывает форма средней части частотной характеристики.
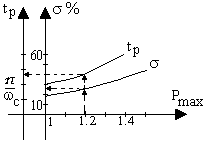
Рис. 6.4. Номограмма В.В.Солодовникова
В связи с этим логарифмическую частотную характеристику разомкнутой цепи системы делят на три области, причем область низких частот в основном определяет точность в установившемся режиме. Область средних частот в основном определяет качество переходного процесса. В частности, частота среза ωс, как уже говорилось, определяет полосу пропускания и длительность переходного процесса. Наклон ЛАХ вблизи частоты среза характеризует колебательность переходного процесса. Так, наклон -20 дб/дек при ω=ωс соответствует свойствам апериодического звена, обеспечивает наименьшую колебательность переходного процесса в замкнутой системе.
Следующей частотной оценкой качества является показатель колебательности - максимальное значение Mmax амплитудной частотной характеристики замкнутой системы
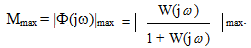 . (6.24)
. (6.24)
Чем меньше запас устойчивости, тем больше склонность системы к колебаниям и тем выше резонансный пик. Считается, что в хорошо демпфированных системах показатель колебательности не должен превосходить значений 1,1÷1,5.
ЦДО ДГТУ © 2012


