6.2. Оценка точности работы систем
Определение установившихся ошибок. Одно из основных требований, которым должна удовлетворять система управления, заключается в обеспечении необходимой точности воспроизведения задающего воздействия в установившемся режиме. Для оценки точности системы определяется установившаяся ошибка, которая может быть получена из выражения (4.4) с помощью теоремы операционного исчисления о конечном значении функции:
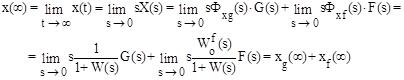 (6.4)
(6.4)
где xg(∞)- установившаяся ошибка от задающего воздействия;
xf(∞)- установившаяся ошибка от возмущающего воздействия.
Если задающее воздействие g(t) имеет произвольный характер, то ошибка системы может быть найдена с помощью коэффициентов ошибок. Изображение ошибки по задающему воздействию имеет вид
Xg(s)= Фxg(s)G(s),
где Фxg(s) - передаточная функция замкнутой системы по ошибке относительно задающего воздействия.
Для получения коэффициентов ошибок передаточная функция Фxg(s) раскладывается в степенной ряд
Фxg(s) = c0 + c1s + c2s2 + c3s3 + ... ,
сходящийся при малых s, что соответствует установившемуся режиму или достаточно большим значениям времени t.
Коэффициенты ci этого ряда называются коэффициентами ошибок и определяются из выражения
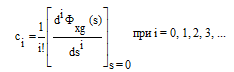 (6.5)
(6.5)
Коэффициенты c0, c1 и c2 называются соответственно коэффициентами позиционной ошибки, скоростной ошибки и ошибки от ускорения.
Выражение для изображение ошибки по задающему воздействию примет вид
Xg(s) = (c0 + c1s + c2s2 + c3s3 + ...)G(s).
Перейдя к оригиналу, выразим установившуюся ошибку через коэффициенты ошибок, задающее воздействие и его производные:
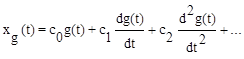 (6.6)
(6.6)
Аналогично можно ввести понятие коэффициентов ошибок по возмущающему воздействию.
Точность в типовых режимах. Для оценки точности системы управления используется величина ошибки в различных типовых режимах, близких к реальным или наиболее трудным. В качестве типовых входных воздействий выбираются воздействия, изменяющиеся по закону g(t)=gn×tn (где n=0,1,2), и гармоническое воздействие g(t)=gm×sinωt.
Рассмотрим установившийся режим системы при постоянных задающем g(t)=g0=const и возмущающем f(t)=f0=const воздействиях. В этом случае ошибка системы называется статической и находится с помощью выражения (6.7):
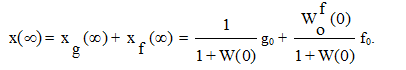 (6.7)
(6.7)
В статических системах управления значение W(0)=k, где k - общий коэффициент передачи разомкнутой системы. При этом составляющая статической ошибки от задающего воздействия
xg(∞)= g0/(1+k). (6.8)
Составляющая статической ошибки от возмущающего воздействия
xf(∞)= kf ×f0/(1+k), (6.9)
где kf - коэффициент передачи разомкнутой системы по возмущающему воздействию.
Из выражений (6.8) и (6.9) следует, что для повышения точности управления необходимо увеличивать общий коэффициент передачи разомкнутой системы k. Тут выявляется противоречие между требованием точности (увеличение k) и устойчивости (ограничение k).
В астатических системах W(0)→∞, поэтому составляющая ошибки xg(∞)= 0.
Вторая составляющая ошибки xf(∞) при W(0)→∞ не всегда обращается в нуль, так как возможен случай, когда и Wfo(0)→∞.
Режим работы при постоянных задающих и возмущающих воздействий наиболее характерен для систем стабилизации.
Рассмотрим теперь установившееся состояние при изменении задающего воздействия с постоянной скорость g(t)=g1×t (где g1=const) и постоянном значении возмущающего воздействия f(t)=f0=const. По (6.4) найдем установившуюся ошибку:
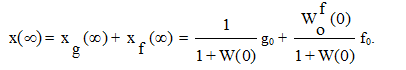 (6.10)
(6.10)
Первый член этого выражения в статической системе при W(0)=k стремится к бесконечности, поэтому система, работающая в режиме слежения с постоянной скоростью, должна быть астатической относительно задающего воздействия. Второе слагаемое определяет статическую ошибку системы от возмущающего воздействия.
Для систем с астатизмом первого порядка установившаяся ошибка от задающего воздействия
xg= g1/kv, (6.11)
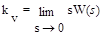
где kv - коэффициент передачи (добротность) системы по скорости.
Ошибка xv(∞)называется скоростной ошибкой от задающего воздействия.
В системах с астатизмом второго порядка и выше скоростная ошибка равна нулю (так как kv→∞), поэтому режим с задающим воздействием, изменяющимся с постоянной скоростью, используется только для оценки точности следящих систем с астатизмом первого порядка.
Рассмотрим установившийся режим в системе при изменении задающего воздействия с постоянным ускорением g(t)=g2×t2/2 (где g2=const) и постоянным значением возмущающего воздействия f(t)=f0=const.
Аналогично определяется установившаяся ошибка по (6.4):
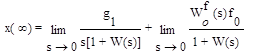 (6.12)
(6.12)
В статических и астатических системах первого порядка первая составляющая ошибки стремится к бесконечности, поэтому этот режим имеет смысл только для следящих систем с астатизмом второго порядка, для которых ошибка по задающему воздействию
xg(∞) (6.13)
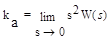
где ka - коэффициент передачи (добротность) системы по ускорению.
Ошибка xg(∞) называется установившейся ошибкой системы от ускорения. Этот режим работы обычно применяется для оценки точности следящих систем с астатизмом второго порядка.
Второе слагаемое, как и в предыдущем случае, определяет статическую ошибку системы от возмущающего воздействия.
Рассмотрим теперь установившийся режим системы управления при изменении задающего воздействия по гармоническому закону
g(t) = gmsinωt.
Для упрощения предположим, что возмущающее воздействие равно нулю.
В линейной системе ошибка в установившемся режиме также изменяется по гармоническому закону с той же частотой:
x(t) = xmsin(ωt+ψ).
Точность системы в этом режиме оценивается по величине амплитуды ошибки. Амплитудные значения связаны между собой модулем частотной передаточной функции замкнутой системы, то есть можно записать
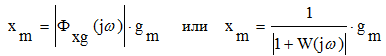 (6.14)
(6.14)
Систему всегда проектируют таким образом, чтобы величина ошибки была меньше задающего воздействия, т.е. выполняется условие |W(jω)|>>1. В связи с этим единицей в знаменателе приведенной выше формулы можно пренебречь. Таким образом, амплитуда ошибки определяется как
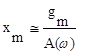 (6.15)
(6.15)
где A(ω) - модуль частотной передаточной функции разомкнутой системы.
Пример. Определить установившиеся ошибки в системе управления, заданной передаточными функциями:
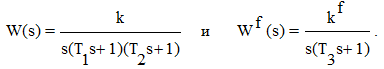
Решение. Найдем установившиеся ошибки системы при различных внешних воздействиях.
1. g(t)=g0×1(t), f(t)=f0×1(t). Тогда G(s)= g0 /s, F(s)= f0 /s.
Установившаяся ошибка от задающего воздействия:
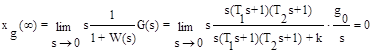
Установившаяся ошибка от возмущающего воздействия:
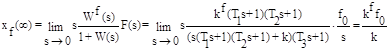
2. g(t)=g1×t, f(t)=f0×1(t). Тогда G(s)=g1/s2, F(s)=f0 /s.
Установившаяся ошибка от задающего воздействия:
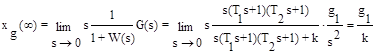
3. g(t)=g2×t2, f(t)=f0×1(t). Тогда G(s)=2g2/s3, F(s)=f0 /s.
Установившаяся ошибка от задающего воздействия:
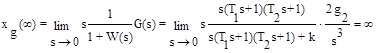
4. g(t) = gmsinωt, f(t)=0.
При k=40 c-1, T1= 0.05 c, T2= 0.01 c, ω=1 c-1 , gm=300 .
Амплитуда ошибки
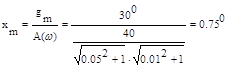
5. g(t) = g0+ g1×t+ g2×t2/2, f(t)=f0×1(t).
Определим коэффициенты ошибок c0, c1, c2. Остальные коэффициенты ошибок находить нет необходимости, так как степень полинома задающего воздействия равняется двум.
Передаточная функция замкнутой системы по ошибке относительно задающего воздействия
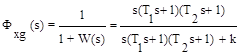 , откуда
, откуда
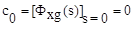 ,
,
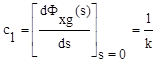 ,
,
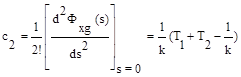 .
.
Установившаяся ошибка от задающего воздействия:
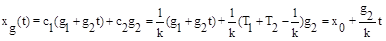 ,
,
где 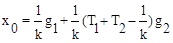 .
.
ЦДО ДГТУ © 2012


