5.4. Частотные критерии устойчивости
Частотные критерии устойчивости базируются на принципе аргумента. Рассмотрим этот принцип, для чего запишем выражение для характеристического вектора, которое получим из характеристического полинома системы (4.2), предварительно разложенного на множители, путем замены p на jω:
D(jω) = an(jω- p1)(jω- p2)...(jω- pn), (5.9)
где pi - корни характеристического уравнения (полюсы системы).
Определим изменение аргумента вектора D(jω) при изменении частоты ω от -∞ до +∞
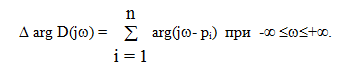
Если корень характеристического уравнения pi расположен на комплексной плоскости слева от мнимой оси, то вектор (jω-pi) поворачивается на угол π, если этот корень находится на комплексной плоскости справа от мнимой оси, то вектор (jω-pi) поворачивается на угол -π. Допустим, что m корней характеристического уравнения расположены справа от мнимой оси, а остальные n-m корней - слева. Тогда изменение аргумента характеристического вектора равно
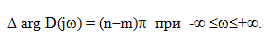
В устойчивой системе m=0, и изменение аргумента характеристического вектора получается следующим:
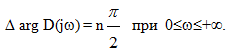
Критерий устойчивости Михайлова.
Из выражения (5.10) следует критерий устойчивости Михайлова, согласно которому изменение аргумента характеристического вектора определяется по годографу вектора, записанному в виде
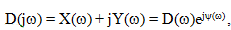 (5.11)
(5.11)
где X(ω) и Y(ω) действительная и мнимая части характеристического вектора, а D(ω) и ψ(ω) его модуль и аргумент.
Формулировка критерия. Для устойчивости линейной системы n-го порядка необходимо и достаточно, чтобы изменение аргумента функции D(jω) при изменении ω от 0 до ∞ равнялось бы n*π/2.
Другими словами, система устойчива, если годограф характеристического вектора (кривая Михайлова), начинаясь на положительной части действительной оси, обходит последовательно в положительном направлении (против часовой стрелки) n квадрантов, где n - порядок характеристического уравнения системы.
На рис.5.8 приведены примеры годографов для устойчивой и неустойчивой систем.
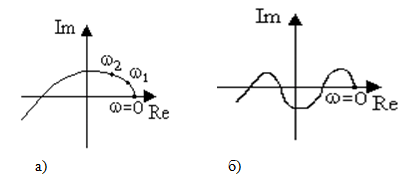
Рис. 5.8. Кривая Михайлова:
а - устойчивой системы 3-го порядка; б - неустойчивой системы
Если годограф проходит через начало координат, то система находится на границе устойчивости. В этом случае
X(ω) = 0 и Y(ω) = 0. (5.12)
Из этих уравнений можно определить значения параметров, при которых система находится на границе устойчивости.
Пример. Исследуем на устойчивость систему, рассмотренную в предыдущем примере, характеристический полином которой имеет вид: D(p) = T1 T
Решение. Найдем годограф характеристического вектора
D(jω) = T1 T2 (jω)3 + ( T1 + T2 )(jω)2 + jω + k.
Откуда
Re D(jω) = X(ω) = k - ( T1 + T2 )ω2;
Im D(jω) = Y(ω) = ω - T1 T2ω3 .
Для того, чтобы система 3-го порядка была устойчива, кривая Михайлова должна последовательно проходить три квадранта (рис.5.9).
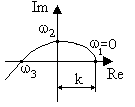
Рис. 5.9. Кривая Михайлова
Найдем условие устойчивости из требования чередования корней 0=ω1<ω2,ω3.
Корень ω2 находится из уравнения X(ω)=0, откуда
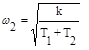
Отсюда первое условие устойчивости: k>0.
Корень ω3 находится из уравнения Y(ω)=0, откуда
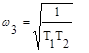
Подставляя эти значения в требуемое условие ω2<ω3, получаем второе условие устойчивости системы
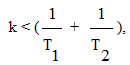
которое, конечно, совпадает с полученным ранее условием устойчивости по критерию Гурвица.
Критерий устойчивости Найквиста.
На практике более широкое по сравнению с критерием Михайлова применение нашел частотный критерий Найквиста, который позволяет судить об устойчивости системы по частотным характеристикам разомкнутой системы. Рассмотрим случай, когда разомкнутая система устойчива и не содержит интегрирующих звеньев.
Введем вектор
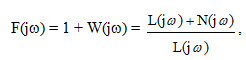 (5.13)
(5.13)
где 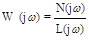 - частотная передаточная функция разомкнутой системы.
- частотная передаточная функция разомкнутой системы.
Числитель (5.13) является характеристическим вектором замкнутой системы, а знаменатель - характеристическим вектором разомкнутой системы. Определим изменение аргумента вектора F(jω) при изменении частоты ω от 0 до +∞ для случая, когда замкнутая система устойчива:
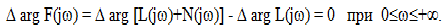
Таким образом, если разомкнутая и замкнутая системы устойчивы, то изменение аргумента вектора F(jω) равно нулю, следовательно, его годограф не охватывает начала координат. В противном случае, когда годограф F(jω) охватывает начало координат, изменение его аргумента не равно нулю и система в замкнутом состоянии неустойчива. Очевидно, что об изменении аргумента вектора F(jω) удобнее судить по годографу частотной характеристики разомкнутой системы, т.е. по ее амплитудно-фазовой частотной характеристике. Действительно, изменение аргумента вектора F(jω) будет равно нулю, если АФЧХ разомкнутой системы не охватывает точку с координатами (-1, j0).
Если система содержит r интегрирующих звеньев, число r которых определяет степень астатизма системы, то начальное значение фазовой частотной характеристики равно -r*π/2, а амплитудной частотной - бесконечности, система в разомкнутом состоянии нейтральна. В таких астатических системах для удобства оценки устойчивости АФЧХ разомкнутой системы дополняют дугой бесконечного радиуса, начинающейся на положительной вещественной полуоси комплексной плоскости. Формулировка критерия устойчивости при этом не изменяется.
Если АФЧХ разомкнутой системы проходит через точку с координатами (-1, j0), то система в замкнутом состоянии находится на границе устойчивости.
Аналогичным образом доказывается критерий Найквиста и для случая, когда разомкнутая система неустойчива.
Формулировка критерия.
1. Если разомкнутая система устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой системы не охватывала точку с координатами (-1, j0).
2. Если разомкнутая система неустойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой системы охватывала точку с координатами (-1, j0) и при изменении частоты от 0 до ∞ оборачивалась вокруг нее против часовой стрелки m раз, где m - число полюсов разомкнутой системы с положительной вещественной частью.
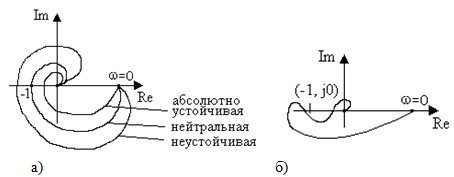
Рис.5.10. АФЧХ статических разомкнутых систем
Графики на рис.5.10,а соответствуют абсолютно устойчивой, нейтральной и неустойчивой системам. Система, АФЧХ разомкнутой цепи которой пересекает вещественную ось только справа от точки с координатами (-1, j0), называется абсолютно устойчивой. В таких системах неустойчивость может наступить только при увеличении общего коэффициента передачи разомкнутой цепи.
Если АФЧХ разомкнутой системы (рис.5.10,б) пересекает вещественную ось и слева от точки с координатами (-1, j0), но при этом число положительных (сверху вниз) переходов характеристики через ось абсцисс левее точки (-1) равняется числу отрицательных переходов (снизу вверх), то систему называют условно устойчивой. Неустойчивой такая система может быть как при увеличении, так и при уменьшении общего коэффициента передачи разомкнутой цепи.
Если передаточная функция разомкнутой системы содержит в своем составе интегрирующие звенья, то АФЧХ начинается в бесконечности ( рис.5.11).
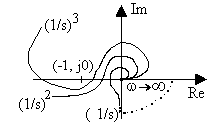
Рис.5.11. АФЧХ астатических разомкнутых систем
Графики на рис.5.11 соответствуют устойчивым системам с первой, второй и третьей степенями астатизма.
ЦДО ДГТУ © 2012


