5.3. Алгебраические критерии устойчивости

Алгебраические критерии позволяют непосредственно по коэффициентам характеристического уравнения судить об устойчивости систем. Различные формы таких критериев рассматриваются в курсе высшей алгебры. В теории управления наибольшее применение из алгебраических критериев устойчивости получили критерий Рауса и критерий Гурвица.

Критерий Рауса.

Линейная система, характеристический полином которой равен

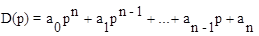
где a₀>0, устойчива, если положительны все элементы первого столбца следующей таблицы

                (5.7)

В первой строке таблицы Рауса расположены четные коэффициенты характеристического полинома, во второй - нечетные. Если степень характеристического полинома - четное число, то последний элемент второй строки равен нулю. Третья и последующие строки определяются следующим образом:

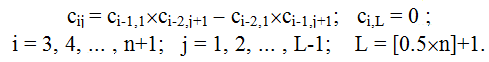
Знак [ ] означает целую часть числа.

Критерий Гурвица.

Линейная система, характеристический полином которой равен

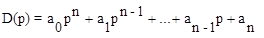
где a₀>0, устойчива, если положительны n главных определителей матрицы Гурвица:

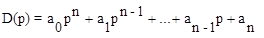                (5.8)

Порядок составления матрицы Гурвица следующий. На главной диагонали записываются все коэффициенты, начиная с первого. Далее заполняются строки: четными коэффициентами по порядку, если на главной диагонали стоит четный коэффициент, и нечетными, если на главной диагонали стоит нечетный коэффициент. Если какой-либо коэффициент отсутствует, то вместо него заносится нуль.

Для оценки устойчивости системы необходимо вычислить определители Гурвица Δ_i (i = 1, 2, ... , n), которые получают из матрицы (5.8) путем отчеркивания равного числа строк и столбцов в левом верхнем углу матрицы.

Система устойчива, если Δ_i > 0 для всех i = 1, 2, ... , n.

Последний определитель Гурвица, как видно из приведенной выше матрицы, равен

Δ_n=a_n*Δ_{n -1}

Поэтому его положительность сводится при Δ_n-1>0 к условию a_n0,

Для систем первого и второго порядка критерий Гурвица сводится просто к положительности коэффициентов a_i.

Если определитель Δ_n=0, то система находится на границе устойчивости. Возможны два случая: апериодическая граница устойчивости, если свободный член характеристического уравнения равен нулю, что соответствует нейтрально устойчивой системе; колебательная граница устойчивости, если определитель Δ_n-1=0. Из условия Δ_n-1=0 можно определить параметры, при которых система находится на границе устойчивости.

Пример. Передаточная функция разомкнутой системы задана в виде: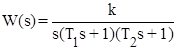 . Исследовать устойчивость системы.

Решение. Характеристическое уравнение замкнутой системы

D(p)=0, где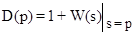

Откуда следует

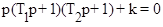
Раскрыв скобки, получим

T₁T₂p³ + (T₁ + T₂)p² + p + k = 0.

Тогда имеем: a₀ = T_{1 T2 ; a1 = (T1 + T2); a2 = 1; a3 = k.}

Коэффициенты характеристического уравнения положительны.

Составляем матрицу Гурвица

и найдем определители этой матрицы. Для устойчивости системы все они должны быть положительными:

Δ₁ = a₁, откуда (T₁ + T₂) > 0;

Δ₂ = a₁×a₂ - a₀ ×a₃, откуда (T₁ + T₂) - kT₁T₂ > 0;

Δ₃ = a₁×a₂×a₃ - a₀×a₃2 = a₃( a₁×a₂ - a₀×a₃ ), откуда a₃ >0 , то есть k > 0.

Условие устойчивости по критерию Гурвица получает вид

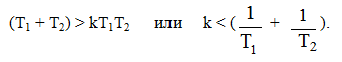
Границы устойчивости:

  1) a_n = 0, k = 0;

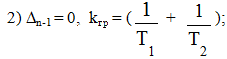
  3) a₀        , T₁T₂ = 0.

Эти три границы устойчивости можно изобразить графически в пространстве параметров k, T1, T₂ и найти области устойчивости системы.

Найдем сначала область устойчивости системы по одному параметру k (общий коэффициент передачи разомкнутой системы). Пространство параметров здесь одна прямая линия, а границы устойчивости - точки на ней: k = 0 и k = k_гр (рис.5.6). Область устойчивости лежит между этими точками.

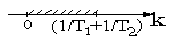
Рис. 5.6. Область устойчивости по одному параметру

Те же границы устойчивости системы можно построить на плоскости двух параметров, например: k и T₁ (рис.5.7). Первая граница k = 0 лежит на оси T₁. Вторая граница 1/T₁ = k - 1/T₂ имеет вид гиперболы с асимптотами k = 0 и k = 1/T₂ . Третья граница T₁ = 0 совпадает с осью k. Штриховка границ сделана в сторону области устойчивости.

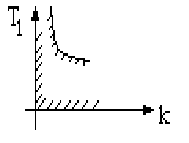
Рис. 5.7. Область устойчивости по двум параметрам

Как видно, при увеличении постоянных времени T₁ и T₂ область устойчивости сужается. Отрицательно влияет на устойчивость также и увеличение общего коэффициента передачи разомкнутой системы k. При любых заданных T₁ и T₂ существует свое граничное значение общего коэффициента передачи k_гр, после чего система становится неустойчивой.

Далее можно построить область устойчивости и в пространстве трех параметров k, T₁, T₂. Границами устойчивости здесь будут являться три координатные плоскости и криволинейная поверхность, сечениями которой как в вертикальных так и в горизонтальных плоскостях будут гиперболы.