4.2. Многомерные системы управления

Многомерные или многосвязные системы - это системы, имеющие несколько управляемых величин, а также несколько задающих и возмущающих воздействий. Многомерная система предполагает наличие многомерного объекта управления (рис.4.6), который характеризуется существованием нескольких входов (точек приложения управляющих и возмущающих воздействий) и нескольких выходов, определяемых управляемыми величинами.

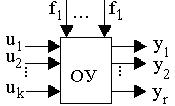
Рис.4.6. Многомерный объект управления

Многомерный объект описывается системой уравнений, которую удобно представлять в матричной форме. В этом случае координатами системы управления являются вектор задающего воздействия G(t), вектор управляемой величины Y(t), вектор управления U(t) и вектор возмущения F(t). При этом

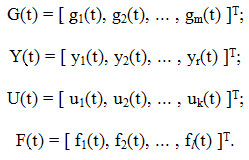
Функциональная схема многомерной системы имеет вид, приведенный на рис.4.7.

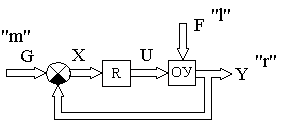
Рис. 4.7. Функциональная схема многомерной системы

Структурная схема изображена на рис.4.8.

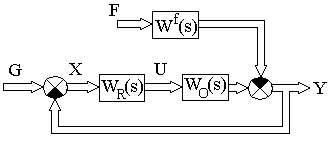
Рис. 4.8. Структурная схема многомерной системы

Здесь W_R(s), W₀(s), W_f(s) - матрицы передаточных функций регулятора и объекта управления системы.

Матричное дифференциальное уравнение линейной многомерной системы, разрешенное относительно управляемой величины имеет вид:

D(p)Y(t) = R(p)G(t) - N(p)F(t), (4.9)

где

квадратная матрица коэффициентов системы (размерность r× r, где r - число управляемых величин), характеризующая свободное поведение системы;

прямоугольная матрица коэффициентов системы (размерность r× m, где m - число задающих воздействий), связывающая задающее воздействие с управляемой величиной;

прямоугольная матрица коэффициентов системы (размерность r× l, где l - число возмущающих воздействий), связывающая возмущающее воздействие с управляемой величиной.

Подвергнув уравнение (4.9) преобразованию по Лапласу, получим матричное операторное уравнение, решение которого определяет изображение управляемой величины

Y(s) = Ф(s)G(s) - Фf(s)F(s), (4.10)

где

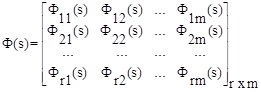
матрица передаточных функций замкнутой системы;

матрица передаточных функций замкнутой системы по возмущающему воздействию.

Здесь Ф_ij(s) - передаточная функция замкнутой системы, связывающая i-ый выход с j-тым входом системы.

Аналогичным образом составляется матричное дифференциаль-ное уравнение, разрешенное относительно ошибки, и определяется изображение рассогласования.