3.2. Типовые динамические звенья и их характеристики
Типовые динамические звенья - это минимально необходимый набор звеньев для описания системы управления произвольного вида.
Типы звеньев систем управления различаются по виду их передаточной функции (или дифференциального уравнения), определяющей все их динамические свойства и характеристики. Классификация основных типов динамических звеньев приведена на рис.3.9.
Основные типы звеньев делятся на четыре группы: позиционные, интегрирующие, дифференцирующие и неминимально-фазовые [1,2]. Позиционные, интегрирующие и дифференцирующие звенья относятся к минимально-фазовым. Важным свойством минимально-фазовых звеньев является однозначное соответствие амплитудной и фазовой частотных характеристик. Другими словами, по заданной амплитудной характеристике всегда можно определить фазовую и наоборот.
Позиционные звенья
В звеньях позиционного, или статического типа, линейной зависимостью y = kx связаны выходная и входная величины в установившемся режиме. Коэффициент пропорциональности k между выходной и входной величинами представляет собой коэффициент передачи звена. Позиционные звенья обладают свойством самовыравнивания, то есть способностью самостоятельно переходить в новое установившееся состояние при ограниченном изменении входного воздействия.
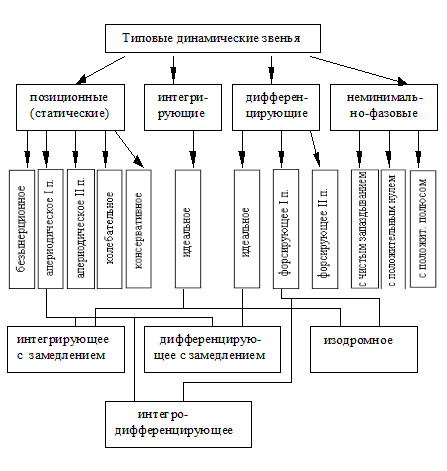
Рис. 3.9. Классификация типовых динамических звеньев
Безынерционное (идеальное усилительное) звено. Это звено не только в статике, но и в динамике описывается алгебраическим уравнением
y(t) = kx(t). (3.14)
Передаточная функция:
W(s) = k. (3.15)
Амплитудно-фазовая частотная характеристика:
W(jω) = k, A(ω) = k, ψ(ω) = 0. (3.16)
Переходная и импульсная функции:
h(t) = k1(t), w(t) = kω(t). (3.17)
Безынерционное звено является некоторой идеализацией реальных звеньев. В действительности ни одно звено не в состоянии равномерно пропускать все частоты от 0 до ∞.
Примерами таких безынерционных звеньев могут служить жесткая механическая передача, часовой редуктор, электронный усилитель сигналов на низких частотах и др.
Апериодическое (инерционное) звено первого порядка. Уравнение и передаточная функция звена:
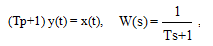(3.18)
где T - постоянная времени, характеризу
Амплитудно-фазовая частотная характеристика:
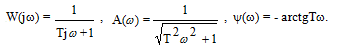(3.19)
Таким образом, апериодическое звено первого порядка является фильтром низких частот.
Переходная и импульсная функции:
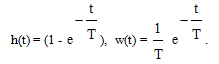(3.20)
Примерами апериодического звена первого порядка могут служить RC цепочка, нагревательный элемент и др.
Апериодическое (инерционное) звено второго порядка. Дифференциальное уравнение звена имеет вид
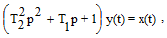(3.21)
причем предполагается, что 2Т2 Т1.
В этом случае корни характеристического уравнения вещественные и уравнение (3.21) можно переписать в виде:
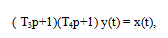(3.22)
где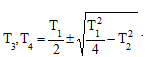 
- новые постоянные времени.
Передаточная функция звена/p>
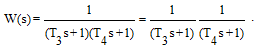(3.23)
Из выражения (3.23) следует, что апериодическое звено второго порядка можно рассматривать как комбинацию двух апериодических звеньев первого порядка.
Примерами апериодического звена второго порядка могут служить двойная RC цепочка, электродвигатель постоянного тока и др.
Колебательное звено. Описывается дифференциальным уравнением
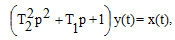(3.24)
при Т1<2T2 корни характеристического уравнения комплексные и уравнение (3.24) переписывают в виде
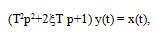(3.25)
где Т - постоянная времени, определяющая угловую частоту свободных колебаний =1/Т;
- параметр затухания, лежащий в пределах 0<<1.
Общепринятая запись передаточной функции колебательного звена имеет вид
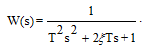(3.26)
Амплитудно-фазовая частотная характеристика звена:
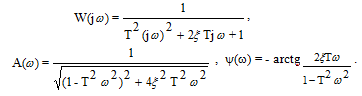(3.27)
Временные характеристики представляют собой затухающие периодические процессы.
Примерами колебательного звена могут служить электрический колебательный контур, электродвигатель постоянного тока, маятник и др.
Консервативное звено. Консервативное звено является частным случаем колебательного при =0. Оно представляет собой идеализированный случай, когда можно пренебречь влиянием рассеяния энергии в звене.
Амплитудно-фазовая характеристика совпадает с вещественной осью. При 0<ω<1/T характеристика совпадает с положительной полуосью, а при ω>1/T - с отрицательной полуосью.
Временные характеристики соответствуют незатухающим колебаниям с угловой частотой 1/T.
Интегрирующие звенья
В звеньях интегрирующего типа линейной зависимостью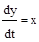 
связаны в установившемся режиме производная выходной величины и входная величина. В этом случае для установившегося режима будет справедливым равенство 
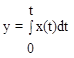, откуда и произошло название этого типа звеньев.
Идеальное интегрирующее звено. Уравнение и передаточная функция имеют вид
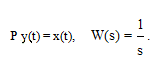(3.28)
Амплитудно-фазовая частотная характеристика:
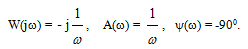(3.29)
Переходная и импульсная функции:
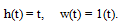(3.30)
Такое звено является идеализацией реальных интегрирующих звеньев.
Примерами идеальных интегрирующих звеньев могут служить операционный усилитель в режиме интегрирования, гидравлический двигатель, емкость и др.
Дифференцирующие звенья
В звеньях дифференцирующего типа линейной зависимостью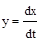 
связаны в установившемся режиме выходная величина и производная входной, откуда и произошло название этого типа звеньев.
Идеальное дифференцирующее звено. Уравнение и передаточная функция имеют вид
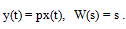(3.31)
Амплитудно-фазовая частотная характеристика:
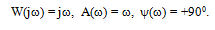(3.32)
Переходная и импульсная функции:
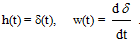(3.33)
Такое звено является идеализацией реальных дифференцирующих звеньев.
Примерами идеальных дифференцирующих звеньев могут служить операционный усилитель в режиме дифференцирования, тахогенератор и др.
Форсирующее (дифференцирующее) звено первого порядка. Дифференциальное уравнение и передаточная функция
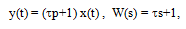(3.34)
где &teta; - постоянная времени дифференцирования.
Амплитудно-фазовая частотная характеристика:
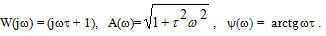(3.35)
Переходная и импульсная функции:
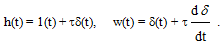(3.36)
Форсирующее (дифференцирующее) звено второго порядка. Уравнение и передаточная функция звена:
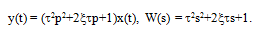(3.37)
Амплитудно-фазовая частотная характеристика:
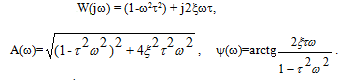(3.38)
Переходная и импульсная функции:
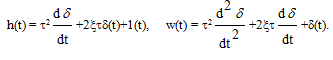(3.39)
Важные комбинации типовых звеньев
Дифференцирующее звено с замедлением или инерционное дифференцирующее звено представляет собой комбинацию идеального дифференцирующего и апериодического звена первого порядка. Уравнение и передаточная функция звена:
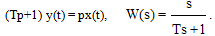(3.40)
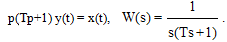(3.41)
Изодромное звено представляет собой комбинацию идеального интегрирующего и форсирующего звена первого порядка. Уравнение и передаточная функция звена:
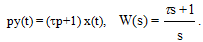(3.42)
Интегро-дифференцирующее звено представляет собой комбинацию форсирующего звена первого порядка и апериодического звена первого порядка. Уравнение и передаточная функция звена:
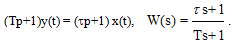(3.43)
Неминимально-фазовые звенья
Неминимально-фазовые звенья - это такие звенья, которые, в отличие от обычных типовых звеньев, при равенстве амплитудных частотных характеристик имеют большие по абсолютному значению фазовые сдвиги. Одной амплитудной частотной характеристике неминимально-фазовых звеньев может соответствовать несколько различных фазовых частотных характеристик.
Звено с чистым запаздыванием. Это такое звено, у которого выходная величина повторяет входную с некоторой задержкой во времени. Уравнение и передаточная функция звена:
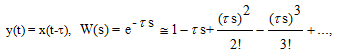(3.44)
где - время чистого запаздывания.
Амплитудно-фазовая частотная характеристика:
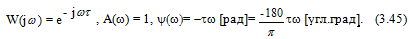(3.45)
Переходная и весовая функции:
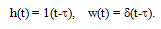(3.46)
Разница между этим звеном и безынерционным, как видим, в величине фазы. Амплитудные же характеристики одинаковы.
Примерами таких звеньев могут служить линия связи, трубопро-вод, транспортер, конвейер и др.
Звено с положительным полюсом. Передаточная функция звена имеет вид
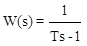(3.47)
Здесь имеется положительный полюс ( корень знаменателя) s1=1/T. В полюсе передаточная функция стремится к бесконечности (W(s)). Амплитудно-фазовая частотная характеристика:
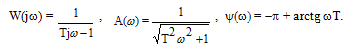(3.48)
Разница между этим звеном и апериодическим первого порядка, как видим, в величине фазы. Амплитудные же характеристики одинаковы.
Звено с положительным нулем. Передаточная функция звена имеет вид
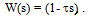(3.49)
Здесь имеется положительный нуль (корень числителя) s1=1/. В нуле передаточная функция равна нулю (W(s)=0).
Амплитудно-фазовая частотная характеристика:
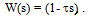(3.50)
Разница между этим звеном и форсирующим первого порядка только в величине фазы. Амплитудные же характеристики одинаковы.
ЦДО ДГТУ © 2012