10.7. Прямой корневой метод синтеза систем управления

Качество процесса управления, как отмечалось в разделе 6.5, определяется расположением корней характеристического уравнения замкнутой системы. В связи с этим разработаны различные корневые методы расчета систем управления. Одним из них является прямой корневой метод синтеза, называемый модальным методом синтеза системы по заданному качеству процесса управления [2]. Вводится целевая функция, которая является функциональным выражением поставленной цели при синтезе системы. Обычно целевую функцию представляют как ограниченную скалярную действительную непрерывно дифференцируемую функцию F = F(q₁, q₂, ..., q_n) искомых параметров q_i (i = 1, 2, ..., n) регулятора системы.

При этом общую задачу рассматривают как выбор вектора параметров q = [q₁, q₂, ..., q_n]_T , оптимизирующего в допустимых пределах значение целевой функции на допустимом множестве Qⁿ.

Однако часто при проектировании системы не проводят подобную оптимизацию, а исходят из удовлетворения заданным требованиям.

В этом случае задача синтеза состоит в том, чтобы, опираясь на ряд качественных показателей системы, найти соответствующее расположение корней характеристического уравнения замкнутой системы λ₁, λ₂, ..., λ_n на комплексной плоскости, а затем найти параметры регулятора, обеспечивающие заданное расположение указанных корней. При этом исходными качественными показателями могут быть, например, вид переходного процесса, время регулирования, колебательность, интегральная квадратичная ошибка и так далее. Указанные требования на одновременное выполнение различных качественных показателей создаваемой системы приводят к задаче выделения на комплексной плоскости соответствующих областей допустимого расположения корней характеристического уравнения замкнутой системы.

Характеристическое уравнение системы D(λ) = 0 (10.26) переписывается в виде

λⁿ +a₁λ^n-1 + a₂λ^n-2 + ... + a_n-1λ +a_n = 0.                           (10.61)

Каждый коэффициент a_i (i = 1, 2, ..., n) является функцией от параметров объекта управления и регулятора, то есть

a_i = a_i(q), i = 1, 2, ..., n,                           (10.62)

где q = [q₁, q₂, ..., q_n]^T - искомый параметрический вектор. Для решения задачи модального синтеза ставится в соответствии с (10.61) и (10.62) желаемый характеристический многочлен

D^*(λ) = ( λ - λ₁^* )×( λ - λ₂^* ) ... ( λ - λ_n^* );

после раскрытия скобок получаем

D^*(λ) = λⁿ +b₁λ^n-1 + b₂λ^n-2 + ... + b_n-1λ +b_n,                           (10.63)

где λ_i^* - желаемые значения корней характеристического полинома, лежащие в заданных пределах:

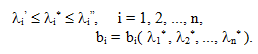                          (10.64)

Приравнивая соответствующие коэффициенты (10.62) и (10.64), получаем

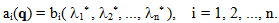                          (10.65)

Таким образом, имеем систему n уравнений с n неизвестными, решая которую непосредственно или численными методами, можно определить все n значений параметров вектора q = [q₁, q₂, ..., q_n]^T.

Очевидно, что независимое назначение всех коэффициентов характеристического уравнения ai (i = 1, 2, ..., n) возможно лишь при числе корректирующих параметров не менее n. Это обстоятельство делает возможным предписанное назначение желаемых корней λ_i (i = 1, 2, ..., n).

В настоящее время для синтеза систем имеются разнообразные программные средства. Примером может служить CLASSiC (Complex Linear Analysis and Structure Synthesis in Control) - программа для персональных компьютеров класса IBM PC, позволяющая строить математические модели, анализировать и синтезировать системы управления со сложной структурой [16].