10.6. Оценивание координат состояния систем

Оценивание координат состояния систем требуется в случае необходимости введения в систему автоматического управления корректирующего сигнала от какой-либо координаты состояния x_i, которая не измеряется как физическая.

Для этого служит косвенная оценка неизмеряемых координат состояния системы путем введения так называемого “наблюдателя” по Калману [2]. Метод оценки вектора состояния дает возможность “восстановить” неизмеряемые координаты вектора состояния в виде X⁾≈X и использовать “восстановленный” вектор состояния системы для решения задачи, например, модального синтеза в пространстве состояний.

Схема оценивания координат состояния реализуется в виде дополнительной динамической аналоговой модели - наблюдателя.

Для получения алгоритма наблюдателя Калмана запишем в векторно-матричной форме уравнения объекта управления

X²=AX + BU                           (10.50)

и управляющее воздействие

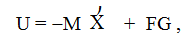                          (10.51)

где G - задающее воздействие;

A, B, M, F - матрицы коэффициентов.

Выходные координаты системы задаются в виде

Y = CX .

Оценка координат состояния системы наблюдателем формируется следующим образом:

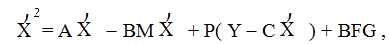                          (10.52)

где P - тоже матрица коэффициентов.

Рассматривая совместно уравнения (10.50), (10.51) и (10.52), получим

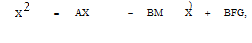                          (10.53)

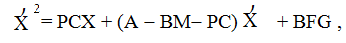                          (10.54)

или в векторно-матричной форме

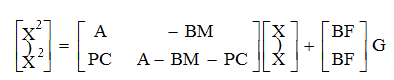
Из полученных уравнений видно, что при использовании наблюдателя порядок всей системы увеличивается до 2n, тогда как n - число координат, которые можно использовать для управления системой, сохраняется.

Характеристическое уравнение системы с наблюдателем имеет вид

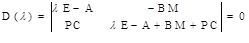                          (10.55)

Для оценки точности работы наблюдателя перейдем к новым координатам в виде ΔX = X - X⁾. Вычитая (10.54) из (10.53), получаем

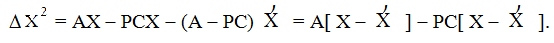
Следовательно,

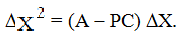                          (10.56)

Из уравнения (10.53), заменяя ΔX = X - X⁾, при отсутствии задающего воздействия G имеем

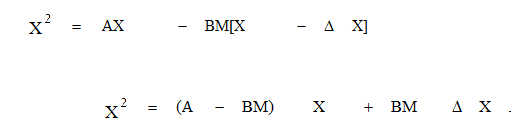                          (10.57)

Уравнения (10.57) и (10.56) в векторно-матричной форме имеют вид

                          (10.58)

Характеристическое уравнение для этой системы будет

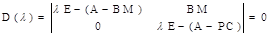
Оно принимает вид

D(λ) = |λE - A + BM|×|λE - A + PC| = 0,

т. е. распадается на два уравнения

|λE - A + BM| = 0,                           (10.59)

|λE - A + PC| = 0,                           (10.60)

Последнее обстоятельство дает возможность независимого модального синтеза как основной системы с координатами вектора X по уравнению (10.59), так и системы определения погрешности ΔX по уравнению (10.60). Требуется, чтобы погрешность наблюдения ΔX(t) быстро затухала во времени.

Существуют и другие схемы наблюдателей, каждый из которых обладает своими особенностями.