Сущность этого способа состоит в том, что при неизменном положении в пространстве заданного оригинала вводится новая дополнительная плоскость проекций, которую располагают так, чтобы оригинал занимал к ней частное положение. Обязательным условием является взаимная перпендикулярность введённой, дополнительной и одной из имеющихся плоскостей проекций (рис. 215, 216, 224).
Так как в машиностроении применяется ортогональное проецирование, то проецирующие лучи параллельны одной из плоскостей проекций, которая остается в паре с новой плоскостью проекций. Расстояние от оригинала до вводимой дополнительной плоскости проекций может быть произвольным.
На примере одной точки изучим операцию замены плоскостей проекций. Пусть дана точка А в системе плоскостей проекций П2 - П1, и требуется построить её проекцию на вновь ведённую плоскость проекций П4. Новую дополнительную плоскость проекций совмещают с плоскостью чертежа вращением вокруг новой оси Х14 - линии пересечения вводимой дополнительной плоскости с существующей, уже совмещённой с плоскостью чертежа. Направление поворота не оказывает никакого влияния на результат. Обычно поворот вводимой дополнительной плоскости проекций осуществляют так, чтобы новые проекции не накладывались на имеющиеся.
Построения на эпюре начинают с того, что проводят новую ось - линию пересечения вводимой плоскости проекций с одной из существующих плоскостей. Положение вводимой плоскости проекций сообщается на чертеже направлением новой оси Х14 (рис. 219, 224).
(Открыть в своём
проигрывателе)
Рис. 219
Вид. 17
При проецировании оригинала на П4 проводим новую линию связи по правилу ортогонального проецирования: на чертеже проекций линия связи всегда перпендикулярна оси проекций. Поэтому новая линия связи перпендикулярна оси Х14. От новой оси - оси Х14, откладываем не изменившуюся координату удаления от плоскости П1 - в данном случае координату высоты точки А, ведь плоскость П4 - вертикальная.
Из приведённых построений складывается следующее ПРАВИЛО: от новой оси по линии связи откладываем расстояние, равное расстоянию от исключаемой оси до исключаемого изображения. Фактически мы оставляем точку фиксируемой относительно одной, остающейся в новой системе плоскости проекций, а от исключаемой проекции берём координату удаления от сохранившейся плоскости проекций - в данном случае от П1.
На рис. 219 при переходе проецирования точки А из системы П2 - П1 в систему плоскостей П1 - П4 мы исключаем плоскость проекций П2, проекцию А2 и ось Х12, но горизонтальная проекция точки А - А1 остаётся. С фронтальной плоскости проекций получаем информацию удаления точки А от П1 - координату ZА, измерив удаление А2 от оси Х12. Эту величину .откладываем на новой линии связи от оси Х14 и получаем А4 - проекцию точки А на П4.
Число преобразований определяется поставленной задачей. На рис. 220 выполнено двойное преобразование исходного чертежа точки А. Второе преобразование выполняем по алгоритму:
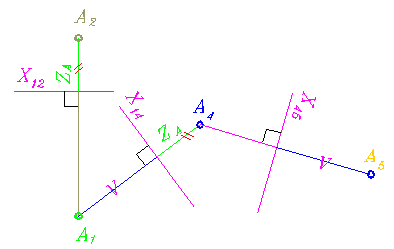
Рис. 220
Очевидно, что для решения задач с одной точкой вводить дополнительную плоскость проекций не имеет смысла. Ведь проекция точки всегда точка. Преобразования чертежа проводят для решения позиционных и метрических задач с линиями и поверхностями.
При любом изучаемом способе преобразования, кроме вращения вокруг прямой уровня, одним преобразованием можно превратить:
Решим эти задачи введением новой дополнительной плоскости проекций (заменой плоскостей проекций).
Задача 1. (рис. 224). Преобразуем прямую общего положения в прямую уровня. Известно, что у прямой уровня одна проекция характерная - параллельна оси, а вторая обладает метрическими свойствами, и, в общем случае, наклонена к оси.
Решение задачи начинаем с проведения новой оси, параллельной одной из проекций прямой. То есть придаём одной из заданных проекций прямой положение характерное для прямой уровня.
Если чертёж прямой общего положения задан безосным, то положение новой оси X12 рационально провести через одну из точек прямой исключаемой проекции, наиболее приближенной к не одноимённой проекции, что сократит построения (в данном случае через A2). Новую ось можно совместить с оставленной проекцией преобразуемой прямой. Сравните построения рисунков 224 и 225.
Выполненные построения позволяют определить величину отрезка прямой общего положения и угол наклона прямой к горизонтальной плоскости проекций. Сопоставьте построения по решению указанных метрических задач способом прямоугольного проецирования (рис. 226).
Для закрепления изучаемого материала решите задачу №30
Задача 2. (рис. 227, 228). Преобразуем прямую уровня в проецирующую. Известно, что у проецирующей прямой одна из проекций обладает метрическими свойствами, вторая вырождена в точку. Причём проекция, обладающая метрическими свойствами перпендикулярна к оси, разделяющей проекции.
Поэтому решение задачи начинаем с проведения новой оси, перпендикулярной к метрической проекции. Исключаемой проекцией прямой уровня будет характерная, которая параллельна исключаемой оси - в данном случае оси Х12. Следовательно, новая проекция прямой будет вырожденной в точку, так как удаление конечных точек A и B от оси одинаково.
Задача 3. (рис. 229). Преобразуем проецирующую плоскость в плоскость уровня. Известно, что у плоскости уровня вырожденная проекция - след, параллельна оси. Поэтому решение задачи начинаем с проведения новой оси, параллельной вырожденной в прямую проекции проецирующей плоскости. Теперь новая проекция плоской фигуры, в рассматриваемом случае - треугольного отсека плоскости, лежащей в заданной плоскости не искажена согласно 7-му свойству ортогонального проецирования. Таким образом, мы нашли натуральную величину треугольника АВС.
Для закрепления изучаемого материала решите задачу №31
Задача 4. Преобразуем плоскость общего положения в проецирующую. Известно, что плоскость перпендикулярна к другой плоскости, если она содержит хотя бы одну прямую, перпендикулярную к другой плоскости. Следовательно, задача сводится к тому, чтобы преобразовать одну из прямых заданной плоскости в проецирующую. Одним преобразованием в проецирующую можно превратить только прямую уровня заданной плоскости.
Поэтому в треугольном отсеке плоскости общего положения АВD (рис. 230) построим прямую уровня - горизонталь h с помощью служебной точки 1, и по отношению к ней решим задачу 2 одного преобразования. Тогда последующее построения приведут к вырожденному в отрезок прямой изображению треугольника ABD
|
Аудио-комментарии |
Тогда новая проекция треугольника непременно окажется вырожденной в прямую линию.
Для закрепления изучаемого материала решите задачу №34
При любом изучаемом способе преобразования, кроме вращения вокруг прямой уровня, двойным преобразованием можно превратить:
Задача 1. Прямую общего положения в проецирующую, последовательно решив первую и вторую задачи одного преобразования (рис. 231, 224, 227, 228).
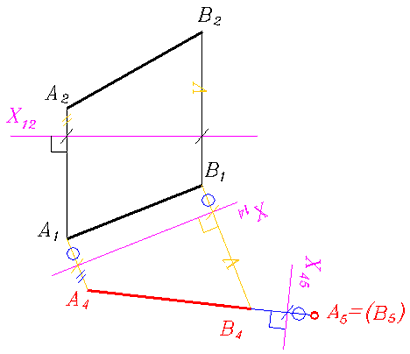
Рис. 231
|
Аудио-комментарии |
Для закрепления изучаемого материала решите задачу №32
Задача 2. Плоскость общего положения преобразовать в плоскость уровня, решив последовательно 4 и 3 задачу одного преобразования (рис. 232, 230, 229).
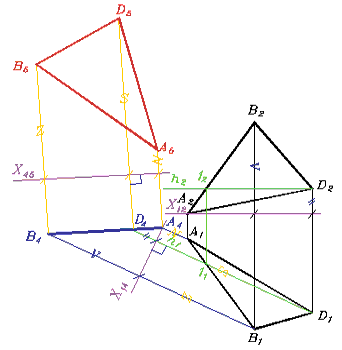
Рис. 232
|
Аудио-комментарии |
Для закрепления изучаемого материала решите задачу №33