9.1. Собственная проводимость полупроводников

Полупроводники высокой степени очистки в области не слишком низких температур обладают электрической проводимостью, обусловленной наличием в них собственных носителей тока – электронов и дырок. Эту проводимость называют собственной проводимостью полупроводников.

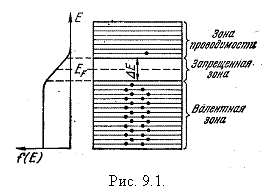
При тепловом возбуждении электрона, находящегося в валентной зоне полупроводника, например, германия или кремния, электрон освобождает состояние в валентной зоне и переходит в зону проводимости, образуя там заполненное состояние. Незаполненное состояние, или вакансия, образующаяся при этом в валентной зоне, называется дыркой. На рис. 9.1 показаны на схеме энергетических зон электрон, перешедший в зону проводимости и образованная им дырка. Распределение электронов по уровням валентной зоны и зоны  проводимости  описывается функцией Ферми - Дирака. Это распределение можно сделать очень наглядным, изобразив график функции распределения  совместно со схемой энергетических зон (рис. 9.1). Соответствующий расчет дает, что у собственных полупроводников отсчитан­ное от потолка валентной  зоны значение уровня Ферми равно   

,                 (9.1)

где ΔE - ширина запрещенной зоны, а m_p и m_e - эффективные массы дырки и электрона. Обычно второе слагаемое пренебрежимо мало, и можно полагать E_p = 1/2ΔE. Это означает, что уровень Ферми лежит посредине запрещенной зоны (см. рис. 9.1). Следовательно, для электронов, перешедших в зону проводимости, величина Е – Е_F мало отличается от половины ширины запрещенной зоны. Уровни зоны проводимости лежат на хвосте кривой распределения. Поэтому вероятность их заполнения электронами можно находить в рамках классической статистики Больцмана, считая газ электронов вырожденным. Положив , получим, что

.                                             (9.2)

В соответствии с наличием в собственном полупроводнике двух типов носителей — электронов и дырок — удельная электропроводность его складывается из проводимости , обусловленной наличием свободных электронов, имеющих концентрацию n_i и подвижность , и проводимости , обусловленной наличием дырок, имеющих концентрацию p_i, и подвижность . Так как n_i = p_i, то полная проводимость собственного полупроводника

.                                    (9.3)

Количество электронов n_i, перешедших в зону проводимости, будет пропорционально вероятности (9.2)

                                       (9.4)

Подвижность носителей тока невырожденного газа в области собственной проводимости определяется выражением (8.15), т.е. более слабой зависимостью от температуры, чем температурная зависимость концентрации носителей тока. Подставив (8.15) и (9.4) в (9.3), получим

,                                                (9.5)

где через  обозначено выражение, стоящее перед экспонентой. Из (9.5) видно, что при  . Следовательно, если бы закономерность (9.5) оправдывалась при сколь угодно высоких температурах, то  выражало бы удельную электропроводность полупроводников при .

Зависимость , от Т удобно представлять в полулогарифмических координатах. Логарифмируя (9.5), найдем

.                                           (9.6)

Если по оси абсцисс отложить 1/T, а по оси ординат , то получится прямая, отсекающая на оси ординат отрезок  (рис. 9.2). Тангенс угла α наклона этой прямой к оси абсцисс равен . Строя такой график, можно определить, таким образом, постоянную  и ширину запрещенной зоны ΔE.
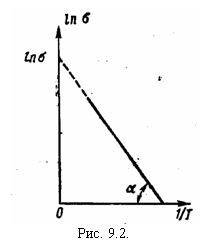Учитывая линейность зависимости от , а также довольно сильное изменение электропроводности, а, следовательно и сопротивление чистых полупроводников, такие полупроводники можно использовать для изменения температуры. Например, сопротивление образца из чистого кремния при повышенной температуре на каждые 10 К уменьшается вдвое. Устройство, изготовленное из чистого полупроводника и использующееся в качестве очень чувствительного электронного датчика температуры, называется термистором.