8.1. Понятие о зонной теории твердого тела

Как мы уже отмечали, приближенное решение общей задачи поведения электронов в кристалле на основе анализа движения одного электрона в поле эффективного потенциала, учитывающего как периодическое изменение потенциальной энергии, обусловленное взаимодействием электрона с атомными остовами, так и согласованное усредненное поле всех остальных электронов.

Однако при качественном анализе соответствующего решения уравнения Шредингера можно привлечь систему эквидистантных одномерных потенциальных ям глубиной U₀ и шириной х₀, которые соответствуют системе последовательно расположенных атомных остовов (тяжелых ионов в случае металлов) и проанализировать, что произойдет с первоначальным энергетическим уровнем основного состояния, существовавший в каждой яме при ее индивидуальном рассмотрении (см. выражение для энергетического спектра микрочастицы в глубоком потенциальном прямоугольном ящике (2.8)). При этом будем учитывать распределение электронов по энергетическим уровням согласно принципу Паули.

Соответствующая система потенциальных ям, естественно, взаимосвязана с потенциальной ямой, которой мы моделировали весь образец металла в квантовой теории свободных электронов в металле и может рассматриваться в виде периодических углублений в потенциальной яме, рассмотренной в п. 7.1.

В качестве первого примера рассмотрим две одномерные прямоугольные потенциальные ямы глубиной U₀ и шириной х₀, соответствующие эффекту, который дают два последовательно расположенных атомных остова. Мы покажем, что первоначальный энергетический уровень основного состояния в каждой из ям, превратится в «зону» с двумя значениями энергии. В случае же N последовательно расположенных прямоугольных ям основному состоянию будет соответствовать зона, содержащая N энергетических уровней. В соответствии с (2.8) энергия уровней в отдельной прямоугольной зоне можно записать приближенно в виде

, где l – ширина ямы.

Если теперь, как показано на рис. 8.1, соединить две ямы в одну, но с удвоенной шириной (l = 2х₀), то мы получим , то есть данному n, например, n=1, будут соответствовать два уровня и .

Соответствующие волновые функци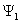и и 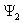будут иметь вид, показанный на рис. 8.1. Если задать глубину потенциальной ямы , то E₁ и Е₂ будут равны соответственно Е₁=0,0246U₀ и Е₂=0,0986U₀.

Если раздвинуть две ямы на достаточно большое расстояние друг от друга оба энергетических уровня практически сливаются, а волновая функция в пределах каждой ямы практически совпадает с волновой функцией основного состояния в случае отдельной ямы.

Итак, расстояние между уровнями энергии, отвечающими волновым функциям 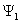и 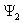, зависит от расстояния между потенциальными ямами. Чем меньше расстояние между ямами, тем сильнее раздвинуты энергетические уровни и наоборот. Этот результат нетрудно обобщить на случай N расположенных друг за другом ям. При этом в окрестности исходного уровня должна образовываться энергетическая зона из N энергетических уровней. Увеличение числа N не приводит к изменению ширины зоны при условии, что расстояние между ямами остается тем же самым, что и характерно для периодического расположения атомов в узлах кристаллической решетки. Напомним, что в одном моле кристалла содержится N=N_A=6,02*10²³ моль^-1 атомов, так что образованную энергетическими уровнями зону можно считать сплошной.

В случае реальных твердых тел одномерную потенциальную яму следует заменить трехмерной потенциальной ямой атома. При сближении N атомов каждое атомное состояние будет превращаться в зону, содержащую N соответствующих энергетических уровней. Чем ближе атомы расположены друг к другу, тем шире зоны. Электронная конфигурация атома 1s²2s²2p⁶3s²... , где 1, 2, 3 … соответствуют главному квантовому числу n, a s, p, d, f … - орбитальному квантовому числу l, а показатели степени заполнению электронами соответствующих энергетических подоболочек, которые и расщепляются в энергетические зоны. Соответствующие энергетические зоны металла натрия в зависимости от межатомного расстояния R в качестве примера приведены на рис. 8.2. Зона 2s располагается при –63,4 эВ, а зона 1s – при –1041 эВ и на рисунке не показаны. Обе эти зоны уже, чем зона 2р.

Для металлической связи характерно столь близкое расположение потенциальных ям, что зона, в которой находится внешний электрон, перекрывается с другими зонами. Это справедливо и для энергетических зон металлического натрия, изображенных на рис. 8.2. Как и в модели свободных электронов, в металле в данном случае имеется неограниченное число свободных состояний, которые может занять внешний электрон.

В некоторых ковалентных кристаллах, например в кремнии и германии, расстояние между атомами таково, что зоны, содержащие валентные электроны не перекрываются. Оказывается, что у кремния заполненная валентная зона и следующая за ней более высокая пустая зона разделены запрещенной зоной шириной 1,09 эВ. В случае германия ширина соответствующей запрещенной зоны составляет 0,72 эВ. Для того, чтобы через кремний и германий мог протекать электрический ток, в пустой зоне должно иметься некоторое количество электронов. Соответственно пустая зона валентных электронов называется зоной проводимости. При комнатной температуре количество электронов, попавших в эту зону проводимости за счет теплового движения невелико. Проводимость германия и кремния значительно ниже, чем у обычного металла. Поэтому эти кристаллы называют полупроводниками. Если же ширина запрещенной зоны кристалла слишком велика, так что теплового движения недостаточно для ее преодоления, то такой кристалл называется диэлектриком. При абсолютном нуле чистые кристаллы диэлектриков и даже полупроводников обладали бы бесконечно большим сопротивлением.

Итак, если придерживаться данных выше определений зоны проводимости, как свободной или частично заполненной зоны валентных электронов, и валентной зоны, как заполненной зоны валентных электронов при абсолютном нуле температуры, можно провести схематическое сравнение энергетических зон у кристаллов, обладающих разной электронной проводимостью, как это сделано на рис. 8.3.

Рис. 8.3. Заполнение зон электронами: E_v – граница валентной зоны, E_c – граница зоны проводимости, E_g – ширина запрещенной зоны.

Большинство энергетических свойств кристалла определяется состояниями электронов, расположенными вблизи поверхности Ферми, которая в общем случае может иметь довольно сложную форму. В первую очередь это относится к явлениям переноса, таким как электропроводность и электронная теплопроводность. Мы при рассмотрении простейших моделей квантовой теории кристаллов пользуемся только одномерным отражением поверхности Ферми в виде уровня или энергии Ферми EF. При этом дополнительная энергия электронной подсистемы, обуславливающая существование упорядоченного потока электронов, может возникнуть только за счет возбуждения электронов при переходе из основного состояния на свободные уровни, незначительно отличающиеся по энергии от исходных. Поэтому надо учитывать только самые верхние частично или полностью заполненные зоны. Нагревание кристалла до определенной температуры T<<T_F= E_F/T или наложение на него внешнего электрического поля могут изменить заполнение электронных состояний только вблизи E_F.