7.2. Работа выхода. Проникновение через барьер

Учитывая отмеченное выше сходство распределения свободных электронов в трехмерной потенциальной яме с распределением микрочастиц в одномерной потенциальной яме можно для графического изображения распределения электронов проводимости в металле воспользоваться энергетической диаграммой, показанной на рис. 7.1. Энергетические уровни электронов ферми – газа, обозначенные такими горизонтальными линиями, заполняют интервал энергии EF от дна потенциальной ямы.

Потенциальная энергия валентных электронов внутри металла меньше, чем вне металла, на величину, равную глубине потенциальной ямы U₀. Изменение энергии происходит на длине порядка нескольких межатомных расстояний, поэтому стенки ямы можно считать вертикальными.

Потенциальная энергия электрона и потенциал той точки, в которой находится электрон, имеют противоположные знаки. Отсюда следует, что потенциал внутри металла больше, чем в непосредственной близости к его поверхности (мы будем для краткости говорить просто “на поверхности”), на величину U₀ / e

Наименьшая энергия, которую необходимо сообщить электрону для того, чтобы удалить его из твердого или жидкого тела в вакуум, называется работой выхода. Работу выхода принято обозначать через e 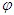, где 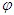- величина, называемая потенциалом выхода.

Как видно из энергетической диаграммы работа выхода А₀ при температуре металла 0К определяется выражением

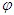A₀ = e= U₀ - E_F            (7.16)

При других температурах работу выхода также определяют как разность глубины потенциальной ямы и уровня Ферми, т.е. распространяют определение (7.16) на любые температуры. Это же определение применяется и для полупроводников.

Покажем, что уровень Ферми зависит от температуры.

Напомним, что количество состояний, приходящихся на интервал энергии dE, равно dV_E (см. формулу (7.8)). Среднее число электронов, находящихся в случае теплового равновесия в этих состояниях, определяется выражением f(E)dV_E . Интервал от этого выражения даст полное число электронов в кристалле

            (7.17)

где n – концентрация электронов.

Подстановка в (7.17) выражения (7.8) и (4.7) дает

            (7.18)

Это соотношение позволяет в принципе найти E_F как функцию Т и n. Интеграл в выражении (7.18) не берется. При условии, что kT<<E_F, удается найти приближенное значение интеграла.

В результате для уровня Ферми получается выражение

            (7.19)

Кроме того, из – за обусловленного тепловым расширением изменения средних расстояний между атомами слегка изменяется глубина потенциальной ямы U₀. Это приводит к тому, что работа выхода немного зависит от температуры.

Работа выхода очень чувствительна к состоянию поверхности металла, в частности к ее чистоте. Подобрав надлежащим образом покрытие поверхности, можно сильно снизить работу выхода. Так, например, нанесение на поверхность вольфрама слоя щелочно – земельного металла (Ca, Sr, Ba) снижает работу выхода с 4,5 эВ (для чистого W) до 1,5 – 2 эВ.

При нагревании металла часть электронов приобретает тепловую энергию, достаточную для того, чтобы преодолеть потенциальный барьер, имеющийся на границе металла. Испускание электронов нагретым металлом называется термоэлектронной эмиссией.

Исследование термоэлектронной эмиссии осуществляется с помощью схемы, изображенной на рис. 7.2. Основным элементом схемы является двухэлектродная лампа, называемая также вакуумным диодом. Она представляет собой хорошо откачанный металлический или стеклянный баллон, внутри которого имеются два электрода – катод К и анод А. Конструктивно электроды могут быть выполнены разными способами.

Катод нагревается током, создаваемым батареей накала Б_Н. Температуру катода можно менять, регулируя с помощью реостата R силу тока накала. На электроды подается напряжение от анодной батареи Б_а Анодное напряжение U_a можно изменять с помощью потенциометра П и измерять вольтметром В. Микроамперметр Г предназначен для измерения силы анодного тока I_a.

При постоянном токе накала катода кривая зависимости силы анодного тока I_a от анодного напряжения U_a имеет вид, показанный на рис. 7.3. Эта кривая называется вольт – амперной характеристикой диода. Различные кривые на рис. 7.3 соответствуют разным температурам катода. При малых значениях U_a эти кривые совпадают.

              

Из рис. 7.3 вытекает, что закон Ома для вакуумного диода не выполняется. Начальный участок кривой довольно хорошо следует полученному теоретически Ленгмюром и Богуславским закону трех вторых. Согласно этому закону сила анодного тока изменяется пропорционально U^3/2. При определенном значении U_a все вылетевшие из катода электроны получают возможность достигнуть анода, и анодный ток достигает насыщения, при этом плотность тока насыщения будет равна . Следовательно, измеряя плотность тока насыщения при различной силе тока накала, можно найти количество электронов, вылетающих с единицы поверхности при разных температурах.

Исходя из квантовых представлений, Дешман получил в 1923 г. для тока насыщения следующую формулу:

            (7.20)

Здесь e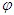 - работа выхода, А – не зависящая от рода металла константа, теоретическое значение которой равно 120 А/см²*К. Экспериментальные значения константы А значительно меньше теоретического и сильно отличаются для разных металлов. Температурный ход тока насыщения формула (7.20) передает вполне удовлетворительно.

Диод пропускает ток только в том случае, когда потенциал анода выше, чем катода. Это свойство диода позволяет его использовать для выпрямления переменного тока.

Установлено, что слабый электронный ток продолжает течь с катода даже при очень низких температурах, когда отсутствуют электроны с тепловыми энергиями, позволяющими преодолеть потенциальный барьер. Это явление называется автоэлектронной эмиссией и представляет собой важное следствие квантовой механики, ниспровергающее классические представления. Оно представляет собой квантовомеханическое свойство проникать сквозь потенциальный барьер или туннельный эффект. Соответствующий эффект рассматривался в п. 2.4 количественно для прямоугольного барьера и качественно для потенциального барьера произвольной формы. В нашем случае потенциальный барьер также имеет сложную форму, на которую влияет и постоянное электрическое поле между катодом и анодом. Проникновение, как мы отмечали в п. 2.4, становится возможным благодаря существованию под барьером волновой функции, “прокладывающей” путь электрону вплоть до преодоления не только высоты, но и ширины соответствующего потенциального барьера. Согласно квантовой механике, вероятность проникновения сквозь барьер при каждом столкновении с ним данного электрона должна составлять . Классическим примером потенциального барьера мог бы служить маленький стеклянный шарик, катающийся внутри чаши. Если выпустить у края чаши, то он будет кататься туда сюда и никогда не выберется из нее. Однако, согласно представлениям квантовой механики, имеется, хотя и очень небольшая вероятность (порядка одного шанса на 10⁽¹⁰²⁹⁾ ) того, что шарик исчезнет из чаши.

На самом деле пример проникновения сквозь потенциальный барьер можно найти и в классической физике. Поскольку уравнение Шредингера и уравнения для световых волн имеют один и тот же вид, можно ожидать, что проникновение через барьер вполне возможно в оптике. Поверхность стеклянной пластинки представляет собой барьер для света, пытающегося выйти из нее наружу. Если свет падает под углом больше критического, то наблюдается полное внутреннее отражение света, т.е. свет не может пройти сквозь барьер. На явлении полного внутреннего отражения основана направленная передача света в волоконных световодах.Волоконный световод представляет собой тонкую гибкую нить (волокно) из оптически прозрачного материала, в частности стекла, внутренняя часть которой (сердцевина) имеет повышенный по сравнению с наружной показатель преломления. Поэтому распространяющиеся в нити лучи (при достаточно малых углах между лучом и осью нити) испытывают полное внутреннее отражение на границе раздела сердцевины и наружной части (оболочки), в результате чего свет локализуется в сердцевине и наружу не выходит. В современных волоконных световодах реализуется минимальная величина оптических потерь и широкая полоса пропускания частот на огромных расстояниях передачи информации.

Интересно, что если вблизи стеклянной пластинки с потенциальным барьером для света поместить другой кусок стекла на расстоянии одной или двух длин волн, то часть света преодолеет барьер и станет распространяться во второй стеклянной пластинке.