7.1. Квантовая теория свободных электронов в металлах

Как мы уже отмечали, металлические решетки представляют собой совокупность положительных ионов, располагающихся в узлах кристаллической решетки, между которыми квазисвободно движутся валентные электроны, обеспечивая взаимодействие между ионами. Масса ионов, расположенных в ионах кристаллической решетки, много больше массы электронов, поэтому в основу теории твердого тела положено адиабатическое приближение. Сущность метода состоит в том, что в нулевом приближении ядра атомов, молекул или ионов считают совершенно неподвижными, а закон движения электронов находят при фиксированных координатах ядер, решая многочастичное уравнение Шредингера для электронов в электро-статическом поле неподвижных ядер. В последующих приближениях можно учесть дополнительные степени свободы, связанные с медленным (адиабатическим) движением ядер, рассматривая эти движения в качестве малых поправок. В случае металлов в качестве медленной подсистемы кристалла, можно рассматривать совокупность ионов, считая, что совокупность валентных электронов образует быструю подсистему кристалла. В соответствии со смыслом адиабатического приближения считают, что электроны движутся в эффективном потенциальном поле, образованном периодической последовательностью тяжелых ионов в фиксированных положениях. Соответствующее поле можно моделировать в виде потенциальных ям, а ионами считать атомы с любой степенью ионизации, т.е. включать в общем случае в рассмотрение как внешние валентные электроны, так и внутренние. Такой переход возможен к рассмотрению электронной подсистемы кристаллов с любым типом связи. Электронная подсистема кристалла, кроме того, заключена внутри потенциального ящика, образованного поверхностью кристалла.

Рассмотрим некоторые особенности поведения электронного газа в кристалле. Первая особенность связана с тем, что электрон является фермионом, вследствие чего система электронов подчиняется принципу Паули и описывается статистикой Ферми – Дирака.

Вторая особенность поведения электронов в твердом теле, имеющая сугубо квантовое происхождение, связана с различным характером взаимодействия внешних валентных и внутренних электронов с атомом или ионом. Соседний атом должен сильнее всего возмущать внешние валентные электроны, расположенные на верхних энергетических уровнях. Для них в отличие от электронов внутренних оболочек возможен с заметной вероятностью туннельный (подбарьерный) переход от одного атома к другому. В результате валентные электроны коллективизируются и занимают общие для системы двух атомов уровни энергии. В металлах коллективизация охватывает внешние валентные электроны всех атомов кристалла, что и позволяет их рассматривать как квазисвободные и занимающие общие для всей системы атомов уровни энергии.

Среди различных методов приближенного решения общей задачи поведения электронов в кристалле плодотворным оказывается метод одноэлектронного приближения. Согласно этому приближению, задача о поведении совокупности электронов заменяется анализом движения одного электрона в поле эффективного потенциала, учитывающего наряду с полем ионов и самосогласованное усредненное поле всех остальных электронов.

Это позволяет в модели свободных электронов в металле рассматривать в качестве глубокого трехмерного потенциального ящика весь образец металла. Для простоты будем считать образец, а следовательно и соответствующий трехмерный потенциальный ящик, имеющим форму куба со стороной L.

Соответствующую задачу мы решали для свободной частицы и в частности для электрона в случае ее одномерного движения в глубоком прямоугольном потенциальном ящике (см. п. 2.2).

Однако в нашем случае надо учесть периодичность кристаллической решетки, что приводит к новому граничному условию для волновой функции = Ae^ikx, которое заключается в требовании, чтобы она была периодической по х с периодом l=L. Легко убедиться, что будет удовлетворять этому условию при значении волнового числа k, равного

            (7.1)

После подстановки (7.1) в (2.8) получим

            (7.2)

Мы видим, что спектр энергии свободных электронов в металле будет дискретным. Учитывая трехмерность потенциального ящика, необходимо вместо одного квантового числа n^* ввести три квантовых числа n_x, n_y, n_z. Для этого вместо волнового числа k_n введем волновой вектор :

Исходя из периодичности трехмерной волновой функции по всем трем координатам x, y и z, запишем условия квантования компонент волнового вектора, которые, естественно совпадают с условием (7.1):

            (7.4)

С учетом (7.1), (7.3) и (7.4) выражение (7.2) запишется в виде

            (7.5)

В объеме образца V=L³ содержится N свободных электронов. Все N электронов стремятся заполнить все энергетические уровни вплоть до уровня Ферми, так как являются фермионами. Распределение электронов по уровням усложняется за счет трехмерности задачи. Чтобы получить полное число заполненных состояний, нам надо сосчитать все возможные комбинации из трех чисел n_x, n_y и n_z. Тогда поверхность равных значений энергии E имеет форму сферы радиуса . При этом любое возможное состояние (или набор трех чисел) изображается точкой в этом воображаемом пространстве. Общее число состояний, энергия которых не превышает E_n^*, с учетом того, что есть еще и спиновое число , равно удвоенному объему сферы.

            (7.6)

Найдя (n_x² + n_y² + n_z²) из (7.5) и подставив в (7.6), получим

            (7.7)

где V=L³ – объем образца металла.

Из соотношения (7.7) вытекает, что

            (7.8)

Здесь dV_E есть число состояний с энергией, заключенной в интервале от E до Е + dE.

Согласно принципу Паули в каждом состоянии, определяемом в нашем случае четырьмя квантовыми числами: n_x, n_y, n_z, m_s может находиться один электрон.

Тогда распределение свободных электронов в металле по энергиям при 0К будет также подчиняться распределению состояний по энергиям (7.8). Введем концентрацию электронов n = N / V , и распределение свободных электронов в металле по энергиям при 0К запишется в виде

где dn(E) - концентрация электронов, энергия которых заключена в пределах от Е до Е + dE; m – масса электрона. Это выражение справедливо при Е < E_F(0), где E_F(0) – энергия при уровне Ферми, т.е. при абсолютном нуле.

Энергия Ферми E_F(0) или максимальная энергия электронов в металле при 0К может быть найдена из формулы (7.7), если взять Е = E_F и ввести концентрацию электронов в формулу (7.7).

Тогда и ,            (7.10)

где n – концентрация электронов в металле.

Поверхность постоянной энергии в k – пространстве (или, что то же самое, в p – пространстве: ), соответствующая значению энергии равному E_F, носит название поверхности Ферми. В случае свободных электронов эта поверхность описывается уравнением

            (7.11)

и, следовательно, имеет форму сферы. При абсолютном нуле температур поверхность Ферми отделяет состояния, заполненные электронами от незаполненных состояний.

Оценим значение E_F(0). Средняя концентрация электронов проводимости в металлах составляет 5*10²⁸ м^–3, тогда по формуле (7.10) найдем

Найдем среднюю энергию электронов при абсолютном нуле.

Суммарная энергия электронов, заполняющих состояния с энергиями от E до E + dE, определяется выражением Edv_E , а соответствующее число электронов будет равно dV_E. Чтобы найти суммарную энергию всех электронов необходимо проинтегрировать от 0 до E_F(0). Точно таким образом можно найти полное число электронов, проинтегрировав от 0 до E_F(0) dV_E. Разделив суммарную энергию всех электронов на полное число электронов, получим среднюю энергию одного электрона:

Подстановка выражения (7.8) для dV_E дает

            (7.12)

Для E_F(0) мы получили значение порядка 5эВ. Следовательно, средняя энергия электронов проводимости при абсолютном нуле составляет примерно 3 эВ. Это огромная величина. Чтобы сообщить классическому электронному газу такую энергию, его нужно нагреть до температуры порядка 25 тысяч кельвин.

Теперь можно объяснить, почему электронный газ вносит очень малый вклад в теплоемкость металлов. Средняя тепловая энергия, равная по порядку величины kT составляет при комнатной температуре 1/40 эВ. Такая энергия может возбудить только электроны, находящиеся на самых верхних уровнях примыкающих к уровню Ферми. Основная масса электронов, размещенных на более глубоких уровнях, остается в прежних состояниях и поглощать энергию при нагревании не будет. Таким образом, в процессе нагревания металла участвует лишь незначительная часть электронов проводимости, чем и объясняется малая теплоемкость электронного газа в металлах.

Число электронов, участвующих в процессе нагревания металла приблизительно равно:

            (7.13)

где N₀ – число электронов проводимости при Т=0К, - величина, называемая температурой Ферми. Следовательно, полная дополнительная энергия электронов при нагревании одного моля металла до температуры Т равна:

            (7.14)

Заменяя N₀ на число Авогадро N_A, мы полагали, что каждый атом металла отдает один электрон в электронную подсистему свободных электронов. Из выражения (7.14) имеем для электронной части молярной теплоемкости:

            (7.15)

т.е. C_V^эл пропорциональна Т. При комнатной температуре C_V^эл примерно в 100 раз меньше классического значения (T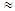300 K, T_F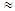25000 K). Электронная теплоемкость не проявляется заметно и при повышении температуры и только при очень низких температурах (Т<1К), когда часть теплоемкости, обусловленная колебаниями решетки, резко уменьшается изменяясь пропорционально Т³ вклад электронов в теплоемкость становится определяющим. Вблизи абсолютного нуля теплоемкость металла пропорциональна температуре. Итак, все особенности электронной теплоемкости металлов получают свое объяснение в рамках квантовой теории свободных электронов в металлах, обусловленной тем, что электронный газ в металлах является вырожденным.