6.3. Теплоемкость кристаллов по Дебаю

В общем случае нельзя приписывать всем фононам одинаковую частоту, как это сделано в модели Эйнштейна. По современным представлениям фонон является квазичастицей, описывающей коллективные колебания атомов в кристалле.

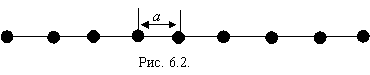
Одним из основных вопросов теории коллективных колебаний атомов кристаллической решетки является вопрос о распределении нормальных (коллективных) колебаний по частотам или, другими словами, вопрос о распределении всех типов фононов по частотам. Рассмотрим сначала простейший случай линейных колебаний линейной цепочки атомов (рис. 6.2). Такую цепочку можно трактовать как струну, в которой можно возбудить стоячую волну. Длины волн нормальных колебаний, которые могут возникать в такой цепочке, равны

            (n=1, 2, 3, …, N),                    (6.7)

где L – длина цепочки, N – число атомов в ней.

Число нормальных колебаний z с длиной волны, равной или большей ln , равно, очевидно, n: .

Аналогичным образом число стоячих волн в трехмерном кристалле объемом V (например, в кубе с ребром L и объемом L3), обладающих длиной волны, равной или большей l, должно быть равно

Более строгий расчет показывает, что

                                          (6.8)

Так как , то  .                           (6.9)

Дифференцируя это выражение, получим

                           (6.10)

Формула (6.10) выражает число нормальных колебаний, заключенное в интервале частот от ω до ω+dω. Функция

                                   (6.11)

определяет плотность заполнения спектрального участка dω нормальными колебаниями, а следовательно, и частотный спектр этих колебаний. Функция  называется функцией распределения нормальных колебаний по частотам.

Так как общее число нормальных колебаний, которое может возникнуть в решетке, равно 3N степеням свободы, то  должно удовлетворять следующему условию нормировки:

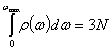,                                          (6.12)

где - максимальная частота, ограничивающая спектр нормальных колебаний сверху.

Подставив (6.11) в (6.12) и проинтегрировав, получим:

                                                    (6.13)

Отсюда находим

                                           (6.14)

Температура

                                                     (6.15)

называется характеристической температурой Дебая. При температуре Дебая в твердом теле возбуждается весь спектр нормальных колебаний или, другими словами, все типы акустических фононов, включая и фонон с максимальной частотой .

Подставив v3 из (6.13) в (6.11), получим

                                             (6.16)

Внутренняя энергия кристалла Е_реш складывается из энергий всех типов фононов и может быть представлена в виде

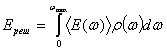                             (6.17)

Подставив в (6.17)  из (6.16),  из (6.2) и N=N_A, придем к формуле внутренней энергии моля кристалла

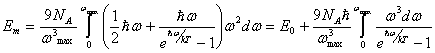 (6.18)

Здесь  - энергия нулевых колебаний кристалла.

Удобно перейти к безразмерной величине , а также введем обозначение  и. Тогда (6.18) перепишется в виде

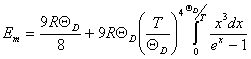                    (6.19)

Рассмотрим отдельно область высоких и низких температур.

1. Область высоких температур (T>>Θ_D).

В этом случае x мало и . Кроме того, очень мал и вклад энергии нулевых колебаний. Тогда

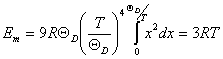
и молярная теплоемкость кристалла .

Таким образом, также как в модели Эйнштейна, мы пришли к закону Дюлонга и Пти.

2. Область низких температур (T<<Θ_D).

Для таких температур верхний предел интегрирования в (6.19) можно заменить бесконечностью. Учитывая, что 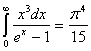, получим

                        (6.20)

Дифференцируя (6.20) по температуре найдем молярную теплоемкость кристалла в области низких температур

.      (6.21)

Мы получили закон Дебая, согласно которому в области низких температур теплоемкость изменяется пропорционально кубу температуры.

Зная температурную зависимость энергии решетки, легко установить, по крайней мере качественно, зависимость концентрации фононного газа от температуры, т.е. числа фононов nф, возбужденных в единице объема кристалла.

В области низких температур, в которой энергия решетки E_реш~T⁴, а энергия фонона , концентрация фононного газа должна быть пропорциональна Т³:

В области высоких температур, в которой E_реш~T, а энергия фононов достигает предельного значения , не зависящего от Т, концентрация фононного газа должна быть пропорциональна Т: n_ф~Т            (6.23).

Теория Дебая хорошо передает температурный ход теплоемкости лишь для тел с простыми кристаллическими решетками. В общем случае необходимо учитывать чрезвычайно сложный спектр колебаний, в котором кроме акустических ветвей возникает и оптическая ветвь. Оптические ветви отличаются от акустических законом дисперсии, т.е. характером зависимости w от волнового вектора .