6.2. Теплоемкость кристаллов по Эйнштейну

Эйнштейн предложил простую модель для объяснения температурного хода теплоемкости кристаллов. Согласно этой модели каждый атом представляет собой осциллятор, колеблющийся с некоторой частотой, одинаковой для всех атомов кристалла. В отличие от классической модели здесь рассматривается квантовый осциллятор, энергия которого может принимать только дискретные значения и определяется выражением (2.9)

             (n = 0, 1, 2,…)

где ω - частота колебаний осциллятора. Газу “осцилляторов” в квантовой механике соответствует  система квазичастиц – фононов, которые являются бозонами и для них характерно распределение Бозе – Эйнштейна (4.3):

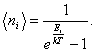
При этом, так как в модели Эйнштейна все фононы имеют одну и ту же частоту, то .

Тогда средняя энергия фонона будет равна

 ,                                               (6.2)

где  - нулевая энергия, которую Эйнштейн не учитывал, так как  ее существование было установлено  значительно позже выдвинутой Эйнштейном модели теплоемкости кристаллов.

Так как фонон имеет три степени свободы, то внутренняя энергия моля кристалла будет равна

                                     (6.3)

Введем параметр , который называют характерис­тической температурой Эйнштейна, тогда:

                               (6.4)

Теплоемкость твердых тел по Эйнштейну определяем, продифференцировав (6.4) по Т:

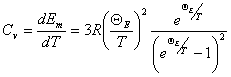               (6.5)

Рассмотрим два предельных случая.

1. Высокие температуры (T>>Θ_E). В этом случае  в знаменателе и  в числителе формулы (6.5). В результате для теплоемкости получается значение

.

Таким образом мы  пришли к закону Дюлонга и Пти. Для большинства твердых тел QЕ лежит в интервале 100 – 300 К.

2. Низкие температуры (T<<Θ_E). В этом случае можно пренебречь единицей в знаменателе выражения (6.5). Тогда формула для теплоемкости принимает вид

                                   (6.6)

Экспоненциальный множитель изменяется значительно быстрее, чем Т². Поэтому при приближении к абсолютному нулю теплоемкость стремится к нулю по экспоненциальному закону, что противоречит экспериментальной зависимости теплоемкости диэлектриков по закону ~T³ и металлов  - по закону ~T. Однако основную роль  в температурную зависимость теплоемкости металлов при сверхнизких температурах вносит электронная система.

Теплоемкость же кристаллической решетки при низких температурах как диэлектриков, так и металлов изменяется по закону: С_реш~T³ и соответствующую экспериментальную зависимость теплоемкости кристаллической решетки удалось объяснить только в модели Дебая.