МЕТОДИЧЕСКИЕ УКАЗАНИЯ
6.1. Классическая теория теплоемкости твердых тел
В XIX в. Дюлонг и Пти при измерении теплоемкости твердых тел эмпирически установили закон: теплоемкость одноатомных кристаллов при комнатной температуре очень близка к значению
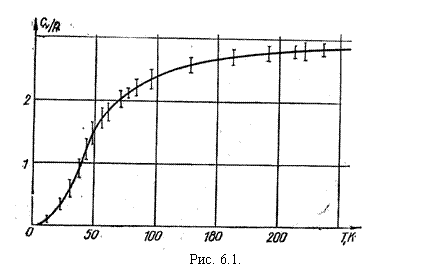
СV = 25 Дж/(моль×К) = 3Rи мало изменяется с повышением температуры, стремясь к указанному значению. Позже экспериментальное исследование поведения теплоемкости при понижении температуры показало, что при низких температурах теплоемкость резко уменьшается и вблизи температуры абсолютного нуля изменяется пропорционально Т3 для диэлектрических кристаллов и пропорционально Т для металлов. На рисунке 6.1 приведена экспериментальная температурная зависимость теплоемкости серебра.
Для объяснения результатов экспериментов по исследованию температурных свойств теплоемкости твердых тел было предложено несколько моделей, которые мы и рассмотрим, начиная с классической, объясняющей справедливость закона Дюлонга - Пти.
Согласно классической модели внутреннего строения твердых тел одноатомный кристалл можно представить себе как совокупность атомов (квазичастиц), колеблющихся в узлах кристаллической решетки под действием квазиупругих сил. Таким образом, твердое тело в этом случае можно представить как совокупность классических осцилляторов, имеющих три колебательных степени свободы, число которых в одном атоме равно числу Авогадро. Применяя для описания поведения такой совокупности осцилляторов классическую теорему о равномерном распределении энергии по степеням свободы, нетрудно найти, что внутренняя энергия моля кристалла будет равна: Em = 3NAkT, а молярная теплоемкость
что прекрасно согласуется с опытными данными. Но с классической точки зрения теплоемкость металлов должна быть значительно выше. В металлах имеются электроны проводимости, с классической точки зрения они обладают тремя поступательными степенями свободы, как свободные частицы (классическая модель электронного газа). Если считать, что число их равно числу атомов, то электроны должны внести в теплоемкость вклад СV = 1,5R, т.е. увеличить ее на 50%. В действительности этого нет, и закон Дюлонга и Пти справедлив и для металлов.
Кроме того, рассмотренная модель не объясняет температурной зависимости теплоемкости, разницы в поведении диэлектриков и металлов при очень низких температурах, а также исключений из закона Дюлонга и Пти: алмаз, бериллий, бор, кремний и алюминий имеют при комнатной температуре теплоемкость, значительно меньшую 3R. При повышении температуры этих веществ их теплоемкость растет, приближаясь к 3R при существенно более высокой температуре. Строгую теорию теплоемкости можно построить лишь на базе квантовой механики.