5.1. Аморфные и кристаллические тела.
Кристаллические решетки

Уменьшение кинетической энергии молекул вещества по сравнению с их потенциальной энергией взаимодействия приводит при некоторых условиях к образованию твердого состояния. Основные виды твердого состояния вещества — кристаллическое и аморфное.

Аморфные вещества, так же как и жидкости, имеют лишь ближ­ний порядок в межмолекулярных взаимодействиях. Теоретическое описание свойств аморфных тел весьма сложно и технология создания аморфных тел с заданными характеристиками часто основывается на эмпирических сведениях и является скорее искусством, чем результатом научных исследований.

Значительно лучше развита физика кристаллического состояния. Кристаллическое состояние — это предмет изучения современной физики твердого тела. В основе теории твердого тела лежит модель бесконечного совершенного монокристалла. Структура такого монокристалла представляет собой непрерывное повторение в пространстве трех измерений одинаковых структурных единиц. Поэтому всегда можно найти три таких направления, при перемещении вдоль которых кристалла параллельно самому себе на отрезки а, b, с будет воспроизводиться конфигурация частиц, образующих кристалл.

Операция перемещения кристалла параллельно самому себе. называемая трансляцией, описывается вектором

,

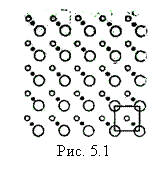где n_i - целые числа. Симметрия кристалла, связанная с его трансляцией, называется трансляционной симметрией. Осуществляя смещение из некоторой точки в пространстве на модуль вектора трансляции при различных n₁, n₂, n₃, можно построить пространственную решетку кристалла. Пространственная решетка — это геометрическое понятие. Ее можно представить себе как результат заполнения трехмерного пространства отдельными ячейками, которые в данном случае носят название элементарных. Элементарной ячейкой мы будем называть такую ячейку, применение к которой операции трансляционной симметрии образует пространственную решетку. Выбор элементарной ячейки не является однозначным. Элементарная ячейка, обладающая наименьшим объемом, называется примитивной ячейкой (рис. 5.1). Объем элементарной ячейки V можно выразить через орты вектора трансляции, именно:

.

Кристаллическую решетку можно получить, связав с каждым узлом пространственной решетки атом, ион или группу атомов, называемую базисом. В простейшем случае базис — это один атом, ион или молекула; но базисом может быть и целая группа атомов. Базис определяется количеством атомов в примитивной ячейке решетки.

Кристаллические решетки могут обладать свойствами симметрии не только к операции трансляции. Возможны и другие геометрические операции, например повороты, отражения, инверсия, повороты с последующим отражением, оставляющие кристаллическую структуру в трехмерном пространстве без изменений. Возникает вопрос сколько может быть элементарных ячеек которые могут непрерывным образом заполнять трехмерное пространство при условии выполнения определенных требований симметрии? На первый взгляд кажется, что таких решеток может быть сколько угодно, однако это не так. Оказывается, что существует всего семь классов кристаллические решеток, которые, как показал русский кристаллограф Е. С. Федоров, могут образовать 230 пространственных решеток с различными типами симметрии.

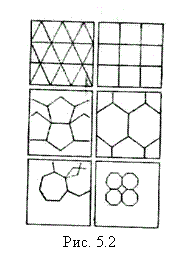
Для того чтобы понять, почему число пространственных решеток кристалла ограничено, обратимся для наглядности к двумерному случаю. Из рисунка 5.2 видно, что не всяким правильным многоугольником можно непрерывным образом заполнить двумерное пространство. Лишь правильный треугольник, квадрат и шестиугольник позволяют это сделать.

Естественно, что определенные ограничения накладываются и на трехмерные решетки, что и обуславливает ограниченность числа пространственных решеток.

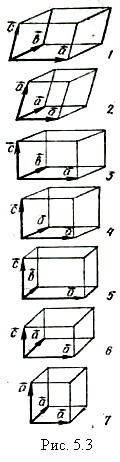
На рисунке 5.3 приведены элементарные ячейки семи классов трехмерных пространственных решеток. Решетка 1, обладающая наинизшей симметрией, называется триклинной. Элементарная ячейка этой решетки — параллелепипед, у которого все стороны, образованные ортами вектора трансляции, разные и все углы между ортами также разные. Тригональной решетке 2 соответствует ячейка, образованная равными по модулю векторами, углы между которыми также равны друг другу. Моноклинная решетка 3 состоит из ячеек, образованных тремя разными векторами, один из которых образует прямой угол с двумя остальными. В ячейке гексагональной решетки 4 один вектор перпендикулярен двум другим, равным по модулю (угол между ними равен 60°). В ромбической решетке 5 элементарная ячейка образована неравными друг другу векторами, углы между которыми прямые. В ячейке тетрагональной решетки 6 углы между векторами сохраняются прямыми, но два вектора равны друг другу по модулю, и, наконец, в кубической решетке 7 элементарная ячейка образована тремя равными по модулю векторами, ортогональными друг другу.

Следует отметить, что в кристалле частицы вещества могут располагаться не только в узлах элементарной ячейки, но и в центре граней (гранецентрированная решетка) или в середине диагональной плоскости, проходящей через вершины (объемно-центрированная решетка). С учетом этих обстоятельств можно указать элементарные ячейки четырнадцати трехмерных решеток, названных решетками Браве.