4.3. Статистика Ферми – Дирака

Частица с полуцелочисленными спинами, в частности свободные электроны в металлах, подчиняются статистике Ферми – Дирака.

,                     (4.5)

где <n_i> - среднее число частиц в состоянии с номером i, E_i – энергия частицы, μ - так называемый химический потенциал, определяемый из условия ∑<n_i> = N.

Частицы, подчиняющиеся статистике Ферми – Дирака называются фермионами. Так как в отличие от статистики Бозе – Эйнштейна в статистику (распределение) Ферми – Дирака единица входит со знаком плюс, то параметр μ в распределении Ферми – Дирака может иметь положительные значения (в данном случае это не приводит к отрицательным значениям чисел <n_i>).

Для фермионов характерно то, что они никогда не занимают состояния, в котором уже находится одна частица. Таким образом, фермионы являются «индивидуалистами».

Именно из этого свойства фермионов следует принцип Паули. В одном и том же атоме (или в какой-либо другой квантовой системе) не может быть двух электронов, обладающих одинаковой совокупностью четырех квантовых чисел:  n, l, m и m_S. Иными словами, в одном и том же состоянии не могут находиться одновременно два электрона. Так как распределение Ферми – Дирака фактически дает функцию распределения электронов по состояниям с различной энергией его часто записывают в виде

.                                   (4.6)

Имеющий размерность энергии параметр μ часто обозначается через E_F и называется уровнем Ферми или энергией Ферми.

В этих обозначениях функция (4.6) имеет вид

.                      (4.7)

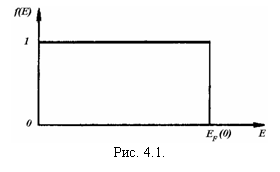Исследуем свойства функции (4.7). При абсолютном нуле f(E)=1, если E < E_F и f(E)=0, если E > E_F.

Таким образом, при 0 К уровень Ферми  E_F совпадает с верхним заполненным электронами уровнем E_F (0). Вид функции f(E) при абсолютном нуле имеет вид, показанный на рис. 4.1.

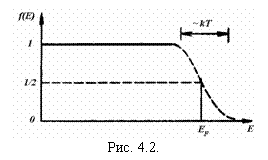
При температурах, отличных от абсолютного нуля, график функции  f(E) имеет вид, показанный на рис. 4.2. Обратим внимание, что при E=E_F функция f(E) = 1/2. Следовательно, уровень Ферми совпадает с энергетическим уровнем, вероятность заполнения которого равна 1/2. В случае больших энергий  (т.е. при E - E_F >>kT, что выполняется в области «хвоста» кривой распределения) единицей в знаменателе можно пренебречь. Тогда распределение электронов по состояниям с различной энергией принимает вид

,

т.е. переходит в классическое распределение Больцмана.

Поведение фермионного газа в сильной степени зависит от соотношения между температурой квантовой системы и температурой Ферми, равной E_F/k. Различают два предельных случая:

1. kT<<E_F. В этом случае фермионный газ называется вырожденным, т.е. он подчиняется квантовой статистике.
2. kT>>E_F. В этом случае фермионный газ называется невырожденным, т.е. он подчиняется классической статистике.

Двояко ведет себя и электронный газ в кристаллах. Температура Ферми для металлов составляет несколько десятков тысяч Кельвин. Поэтому в металле электронный газ практически всегда является вырожденным.

Во многих полупроводниках уже при комнатной температуре и подчиняется классической статистике. электронный газ является невырожденным