ОК-3. МОМЕНТ ИМПУЛЬСА В КВАНТОВОЙ ТЕОРИИ. СПИН

Момент импульса системы классических частиц является суммой моментов импульсов отдельных частиц:

Момент импульса отдельной классической частицы

                                            (3.1)

Применительно к моменту импульса в квантовой механике вводятся четыре оператора: оператор квадрата момента импульса и три оператора проекций момента на оси координат ,  и . Оказывается, что одновременно могут иметь определенные значения лишь квадрат момента импульса L² и одна из проекций момента импульса на координатные оси L_z. Две другие проекции совершенно неопределенны. Это означает, что «вектор» момента импульса не имеет определенного направления и не может быть изображен как в классической механике, с помощью направленного отрезка прямой.

Решение уравнения является очень трудным. Поэтому мы ограничимся конечным результатом: собственные значения оператора квадрата момента импульса равны

                           (l = 0, 1, 2 …).

Здесь l – азимутальное (орбитальное) квантовое число. Модуль момента может иметь только дискретные значения, определяемые формулой

                 (l = 0, 1, 2 …).            (3.2)

Для оператора проекции момента импульса также записывается уравнение . Решение этого уравнения дает дискретные значения и для проекции момента импульса

                     (m= 0, ±1, ±2, …±l).     (3.3)

m – называется магнитным квантовым числом.

Соседние значения магнитного числа  по величине всегда отличаются на единицу и спектр значений числа m симметричен относительно нуля (см. рис. 3.1).

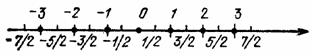
Рис. 3.1.

Теми же свойствами обладает любой набор полуцелых чисел, так же симметричных относительно нуля и содержащий все полуцелые числа, которые существуют между границами набора. Из других чисел наборов с такими свойствами образовать нельзя.

При полуцелом m возникает знаковая неоднозначность волновой функции. Так, если m = ½, то для двух физически эквивалентных углов φ и φ + 2Π   и , то есть возникают разные по знаку волновые функции Ψ и -Ψ, которые физически равноправны. Что касается квантовомеханической вероятности, то будет один и тот же, то есть состояния с Ψ и -Ψ равноправны. Знаковая неопределенность волновой функции означает, что у квантовых частиц есть степени свободы, отличные от характеризующих обычно положения частиц в пространстве.

Момент импульса, связанный с этой дополнительной степенью свободы частицы называется спином частицы.  Впервые это понятие было введено в физику в 1925 г. Дж. Уленбеком и С. Таудсмитом. Подчеркнем, что спин – существенно квантовая величина, не имеющая классического аналога.

В частности, частица со спином вовсе не является системой, подобной вращающемуся на одном месте волчку. Спин – это внутреннее свойство квантовой частицы, характеризующее ее равноправно с такими величинами, как, например, масса и заряд частицы.

Как собственный момент импульса, спин задается неотрицательным числом m_S таким, что

,                             (3.4)

где m_S принимает 2S+1значение: m_S = -S, -S+1,…,S-1,S для электрона (mS = ±S =±1/2). Абсолютное значение спина

                                               (3.5)

Число S принимает не только целые, но и полуцелые значения:

Число m_S называется магнитным спиновым числом, а S – просто спиновым числом. Называя спин, также указывают только число S. Спины электрона, протона и нейтрона одинаковы и равны ½.

Спины фотона и фонона целочисленны.

Бесспиновыми частицами являются пионы. Наличие спина у частиц подтверждено рядом экспериментов.