2.4. Туннельный эффект

Неквантовая  частица не может находиться там, где её потенциальная энергия U(x) превышает полную энергию E. Квантовая частица этой способностью обладает из-за того, что существует отличная от нуля вероятность проникновения частицы через потенциальный барьер, т.е. в область, в которой U(x) > E.

Оценим эту вероятность. Для этого рассмотрим следующую задачу. Пусть квантовая частица с массой m, двигаясь вдоль оси X слева направо, сталкивается с потенциальным барьером конечной высоты  U₀:

,

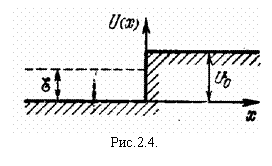
причем энергия частицы E меньше высоты барьера U₀ (рис. 2.4). При x > 0, т.е. в области, в которую неспособна проникнуть неквантовая частица, уравнение Шредингера имеет вид

, где .

Решениями этого уравнения являются две экспоненты: .

Экспонента с положительным показателем физического смысла не имеет и должна быть отброшена, так как предсказывает неограниченный рост вероятности обнаружения частицы за барьером с увеличением глубины проникновения x. Следовательно, при x > 0 частица с энергией E < U₀  имеет волновую функцию Ψ(x), которая изменяется как . Поэтому при x > 0 координаты частицы распределены с плотностью

,   (2.10)

где w(0) равно значению при x = 0.

Мы видим, что с увеличением глубины проникновения x плотность вероятности w(x) убывает экспоненциально. Это убывание происходит тем быстрее, чем больше разность: U₀ –E. Согласно (2.10) на глубине проникновения

плотность вероятности уменьшается в е раз.

Например, для электрона (m = 10^-30 кг), для которого U₀ –E ≈10^-3 эВ = 1,6 ×10^-22 Дж, глубина проникновения

A

Так, на расстояние такого порядка удаляются от поверхности металла электроны проводимости, энергия которых примерно на 10^-3 эВ меньше глубины потенциальной ямы, удерживающей электроны внутри металла. Яма создается взаимодействием электрона с положительными ионами, образующими кристаллическую структуру металла. Глубина проникновения электрона уменьшается на порядок, если разность U₀ –E возрастает до 0,4 эВ.

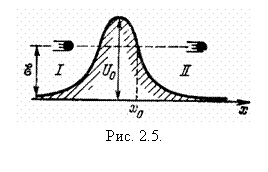
Способность квантовых частиц двигаться через потенциальный барьер приводит к туннельному эффекту. Он заключается в проникновении частицы из одной области в другую область, отделенную от первой потенциальным барьером, даже в том случае, когда энергия частицы  E меньше высоты разделяющего барьера U₀ (рис. 2.5). Такое  проникновение оказывается возможным благодаря существованию под барьером волновой функции, «прокладывающей» путь частице вплоть до точки x₀ и правее этой точки. Туннельный эффект наблюдается и в твердых телах.