МЕТОДИЧЕСКИЕ УКАЗАНИЯ
2.3. Квантовый гармонический осциллятор
Пространственно-ограниченным является движение квантового гармонического осциллятора. Гармоническим осциллятором называют частицу, совершающую одномерное движение под действием квазиупругой силы. Если частота колебаний равна ω, то потенциальная энергия гармонического осциллятора равна
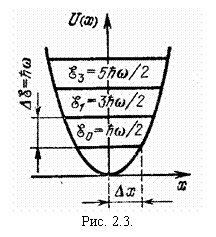
где m – масса осциллирующей частицы. Графиком U(x) является параболическая яма, изображенная на рис. 2.3.
Стационарные состояния квантового осциллятора описываются такими решениями уравнения Шредингера
![]() , которые достаточно быстро убывают при
, которые достаточно быстро убывают при ![]() . Необходимость в этом требовании обусловлена тем, что на сколь угодно больших расстояниях потенциальная энергия частицы неограниченно возрастает.
. Необходимость в этом требовании обусловлена тем, что на сколь угодно больших расстояниях потенциальная энергия частицы неограниченно возрастает.
Нахождение волновых функций осциллятора является сложной математической задачей, изложение которой выходит за рамки этого пособия. Поэтому, опуская решение, приведем только энергетический спектр. Он имеет вид
где n – любое целое неотрицательное число. Спектр (2.9) также показан на рис. 2.3. Этот спектр дискретен и ограничен снизу значением энергии ![]() , которое является основным уровнем квантового осциллятора. В спектре (2.9) промежутки
, которое является основным уровнем квантового осциллятора. В спектре (2.9) промежутки ![]() между соседними уровнями не зависят от квантового числа n, т.е. одинаковы. Такое расположение уровней в спектре называется эквидистантным. Мы видим, что квантовая теория последовательно объясняет существование квантов энергии колебаний.
между соседними уровнями не зависят от квантового числа n, т.е. одинаковы. Такое расположение уровней в спектре называется эквидистантным. Мы видим, что квантовая теория последовательно объясняет существование квантов энергии колебаний.
Так как основной уровень E0 > 0, то квантовый осциллятор остановить нельзя. Например, из-за этого даже при температуре абсолютного нуля не прекращаются колебания кристаллических решеток.
Квантовые колебания с минимальной энергией называются нулевыми. Их существование прямо связано с соотношением неопределенностей: импульс-координата. Чтобы это подтвердить, произведем оценку неопределенности координаты Δx и неопределенности импульса Δp в основном состоянии осциллятора. В этом состоянии значения координаты x и значения импульса p разбросаны около своих минимальных средних значений, равных нулю. Поэтому с точностью до порядков величин x ≈ Δx и p ≈ Δp. Следовательно
Выражая отсюда Δx и Δp, получаем ![]() , что согласуется с соотношением неопределенностей импульс-координата.
, что согласуется с соотношением неопределенностей импульс-координата.
Понятие о квантовом осцилляторе играет важную роль в физике тех явлений, которые обусловлены колебаниями микроскопических объектов. Осциллятор с частотой ω(k) – элементарная форма движения атомов в кристалле, структурная единица колебательного движения атомов кристалла. Каждый осциллятор движется независимо от остальных. Поэтому энергия колебательного движения атомов твердого тела есть сумма энергий отдельных осцилляторов. Итак, «с точки зрения» колебательной энергии кристалла твердое тело можно рассматривать как газ «осцилляторов».