2.2. Одномерное  движение квантовой частицы в глубоком,
прямоугольном потенциальном ящике

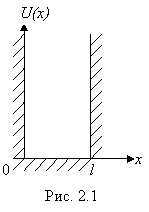
Простейшим примером пространственно-ограниченного квантового движения является одномерное движение квантовой частицы в очень глубокой потенциальной яме с вертикальными стенками. В этом силовом поле график потенциальной энергии частицы U(x) имеет вид, показанный на рис. 2.1. Частица движется свободно на участке 0<x<l, на концах которого она сталкивается с абсолютно твердыми стенками. Их непроницаемость выражается в неограниченном возрастании U(x) в точках x=0 и x=l. Так как частица не выходит из промежутка , то распределение её координат вне этого промежутка отсутствует. Следовательно, уравнение Шредингера должно быть дополнено граничными условиями.

                                            (2.3)

В области, где  Ψ не равна тождественно нулю, будет справедливо стационарное уравнение Шредингера для свободной частицы (2.1). Введем волновое число , тогда уравнение (2.1) запишется в виде

.                             (2.4)

Как мы уже отмечали, частным решением этого уравнения будет функция , где A=const. Уравнение (2.4) напоминает внешне дифференциальное уравнение гармонических колебаний, и его решение будем искать в виде 

.         (2.5)

Постоянные k и α должны удовлетворять граничным условиям (2.3). Прежде всего, из условия  Ψ(0)=0 получаем  Ψ(0)=Asinα=0,   откуда следует, что a  должно быть равно нулю. Далее, должно выполняться условие:   Ψ(l)=Asinkl=0, что возможно лишь в случае, если

 (n = 1, 2, 3 …)                      (2.6)

(n = 0 отпадает, поскольку при этом получается   - частица нигде не находится). Тогда     

Подчинив эту функцию условию нормировки

и вычисляя интеграл, находим, что . Следовательно,

                             (2.7)

Выражая энергию E через волновое число, находим энергетический спектр частицы в неограниченно глубокой потенциальной яме:

                           (2.8)

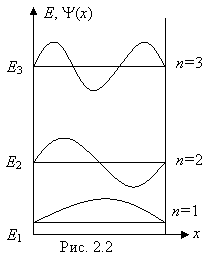
Этот спектр изображен на рис. 2.2. Мы видим, что он дискретен, и ограничен снизу.

Число n, определяющее вид волновой функции и энергию частицы в состоянии с  этой  волновой функцией, называется квантовым числом системы.

Графики волновых функций (собственных) также изображены на рис. 2.2.
В спектре (2.2) основной уровень .

Это неравенство означает невозможность остановки частицы, так как её кинетическая энергия не может быть меньше E₁. Соответственно, неопределённость Δp импульса частицы не может быть меньше величины .

Но в яме шириной l  положение частицы определено с точностью Δ x ≈ l. Следовательно, , что находится в полном согласии с соотношением неопределенностей импульс-координата.

Полученные решения уравнения Шредингера применимы к реальным движениям квантовой частицы между отражающими поверхностями при условиями, что деформация стенок при ударе частицы является упругой и ничтожно малой по сравнению с шириной ямы. Так, например, сталкиваются с границей металла электроны проводимости, если работа выхода из металла достаточно велика.