Применение логики предикатов в математике

I. Применение языка логики предикатов для записи математических предложений, определений.

Пример 8. Записать на языке логики предикатов определение предела числовой последовательности.

Решение. Число а является пределом числовой последовательности (an) тогда и только тогда, когда для любого положительного числа 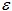существует такой номер n0 , что для всех натуральных чисел, больших или равных n0, справедливо неравенство .

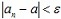Используя язык логики предикатов, можно записать это определение в компактной форме: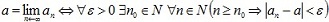

II. Построение противоположных утверждений.

II.Пусть дано некоторое математическое утверждение А. Противоположным утверждением для 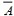будет утверждение. Логика предикатов позволяет путем равносильных преобразований формулы А придать ей хорошо обозримый вид.

Пример 9. Построим утверждение, противоположное определению пределу числовой последовательности.

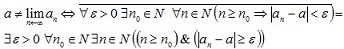
III. Прямая, обратная и противоположная теоремы.

Рассмотрим четыре теоремы:

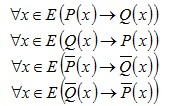
Определение 6. Пара теорем, у которых условие одной является заключением второй, а условие второй является заключением первой, называются взаимно обратными друг другу.

Теоремы (1) и (2), а также (3) и (4) - взаимно обратные теоремы. При этом, если одну из них называют прямой теоремой, то вторую называют обратной.

Определение 2. Пара теорем, у которых условие и заключение одной являются отрицанием соответствующего условия и заключения другой, называются взаимно противоположными.

Так, теоремы (1) и (3), а также (2) и (4) являются взаимно противоположными.

Пример 10. Для теоремы: «Если четырехугольник является прямоугольником, то в четырехугольнике диагонали равны» сформулируйте теоремы (2) - (4).

Решение. Пусть Е = {x} - множество всех четырехугольников на плоскости, Р(x) - свойство х быть прямоугольником, Q(x) - свойство х иметь равные диагонали. В сформулированной теореме Р(х) является условием, a Q(x) - заключением. Поэтому теорема (2), обратная данной , формулируется так: «Если в четырехугольнике диагонали равны, то четырехугольник является прямоугольником»; теорема (3), противоположная прямой, формулируется так: «Если четырехугольник не является прямоугольником, то в четырехугольнике диагонали не равны», теорема (4), противоположная обратной, формулируется так: «Если в четырехугольнике диагонали не равны, то четырехугольник не является прямоугольником».

Задание 8 Запишите на языке логики предикатов определения:

1) линейно упорядоченного множества (упорядоченное множество называется линейным, если для любых элементов этого множества х и у либо х = у , либо х < у, либо х>у);

2) ограниченной функции (функция f(x) называется ограниченной на множестве М, если существует такое неотрицательное число L, что для всех хМ справедливо неравенство );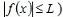

3) четной функции (функция f называется четной, если область ее определения симметрична относительно начала координат и для каждого х из области определения справедливо равенство f(-x)=f(x)) ;

4) периодической функции (функция f называется периодической, если существует такое число Т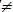 0, что при любом х из области определения f элементы х-Т и х + Т также принадлежат этой области, и при этом выполнено равенство f(x±T) = f(x));

5) возрастающей функции на множестве М (функция f называется возрастающей на множестве М, если для любых чисел х1 и х2, принадлежащих множеству М, из неравенства х1 <х2 следует неравенство f(x1)< f(x2)).

Задание 9: Постройте следующие утверждения:

1) Упорядоченное множество не является линейным?

2) Функция не является ограниченной?

3) Функция не является четной?

4) Функция не является периодической?

5) Функция не является возрастающей на множестве М?

Задание: Доказать несправедливость утверждений:

1. «Если функция непрерывна в точке х0,то она и дифференцируема в этой точке.»

2) «Если в четырехугольнике диагонали равны, то четырехугольник является прямоугольником.»

3. «Если функция интегрируема на [а,b], то она непрерывна на нем.»

4) «Если числовая последовательность имеет предел, то она монотонна.»

5) «Если числовая последовательность ограничена, то она имеет предел.»

6) «Если дифференцируемая функция у = f(x) имеет в точке х0 первую производную равную нулю , то точка х0 - точка экстремума функции.»

Задание 10: Запишите символически следующие суждения:

1) "все судьи - юристы, но не все юристы – судьи”;

2) “Судья, являющийся родственником потерпевшего, не может участвовать в рассмотрении дела. Судья X - родственник потерпевшего. Следовательно, судья X не может участвовать в рассмотрении дела.”

3) “К уголовной ответственности привлекаются лица, совершившие тайное похищение личного имущества граждан. Обвиняемый X не совершал тайного похищения личного имущества граждан. Следовательно, обвиняемый X не может быть привлечен к уголовной ответственности”.

4) “Если иск предъявлен недееспособным лицом, то суд оставляет иск без рассмотрения. Иск предъявлен недееспособным лицом. Следовательно, суд оставляет иск без рассмотрения”.