Равносильные формулы логики предикатов.
Определение 5. Две формулы логики предикатов А и В (A B) называются равносильными на области М, если они принимают одинаковые значения при всех значениях входящих в них переменных, отнесенных к области М. B) называются равносильными на области М, если они принимают одинаковые значения при всех значениях входящих в них переменных, отнесенных к области М.
Две формулы логики предикатов А и В называются равносильными, если они равносильны на всякой области.
Все равносильности алгебры высказываний верны, если в них вместо переменных высказываний подставить формулы логики предикатов. Но, кроме того, имеют место равносильности самой логики предикатов.
Пример 5. Упростить формулу: 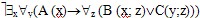 . .
1) выполнить операцию отрицания формулы:
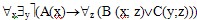
2) удалить логическую связку “ ”: ”:
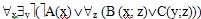
3) выполнить операцию отрицания формулы:
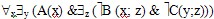
4) перенести квантор 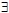 z влево: z влево:
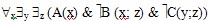
Пример 6. Доказать равносильность 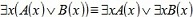
Решение. Для доказательства равносильности достаточно рассмотреть два случая:
1. Пусть предикаты А(х) и В(x) тождественно ложны. Тогда будет тождественно ложным и предикат A(x) 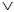 B(x). При этом будут ложными высказывания B(x). При этом будут ложными высказывания 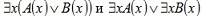
2. Пусть теперь хотя бы один из предикатов (например, A(x)) не тождественно ложный. Тогда будет не тождественно ложным и предикатA(x) 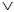 B(x). При этом будут истинными высказывания B(x). При этом будут истинными высказывания 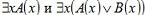 а, значит, будут истинными и исходные формулы. Следовательно, а, значит, будут истинными и исходные формулы. Следовательно, 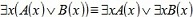 . .
Задание 5: Доказать равносильности логики предикатов:
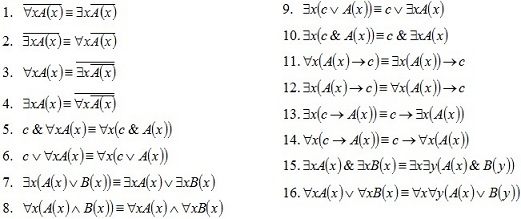
Задание 6: Упростить следующих формул:
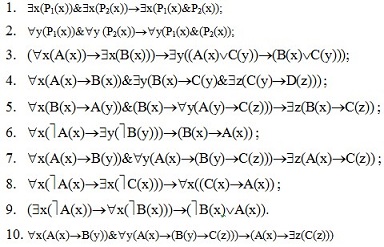
|
