Понятие предиката. Логические и кванторные операции над предикатами.
Определение 1. Одноместным предикатом Р{х) называется всякая функция одного переменного, в которой аргумент х пробегает значения из некоторого множества М, а функция при этом принимает одно из двух значений: истина или ложь.
Множество М, на котором задан предикат, называется областью определения предиката.
Множество 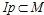 , на котором предикат принимает только истинные значения, называется областью истинности предиката Р(х). , на котором предикат принимает только истинные значения, называется областью истинности предиката Р(х).
Предикат Р(х) называется тождественно истинным (тождественно ложным) на множестве М, если Ip=M 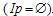 . .
Определение 2. п-местным предикатом называется всякая функция п переменных Q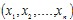 определенная на множестве M=M1*M2*...*Mn и принимающая на этом множестве одно из двух значений: истина или ложь. определенная на множестве M=M1*M2*...*Mn и принимающая на этом множестве одно из двух значений: истина или ложь.
Говорят, что предикат Р{х) является следствием предиката Q(x) (Q(X) 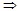 Р(х)), если Iq Р(х)), если Iq 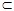 Ip ; и предикаты Р(х) и Q(x) равносильны (Q(X) Ip ; и предикаты Р(х) и Q(x) равносильны (Q(X)  Р(х)), если Iq=Ip Р(х)), если Iq=Ip
Пример 1. Среди следующих предложений выделить предикаты и для каждого из них указать область истинности, если М = R для одноместных предикатов и M = R * R для двухместных предикатов:
1) x + 5 = 1. Предложение является одноместным предикатом P(x),Ip={-4};
2) при х=2 выполняется равенство 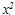 -1=0. Предложение не является предикатом. Это ложное высказывание; -1=0. Предложение не является предикатом. Это ложное высказывание;
3)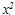 -2x+1=0. Предложение является одноместным предикатом P(x),Ip={1}; -2x+1=0. Предложение является одноместным предикатом P(x),Ip={1};
4)(х+2)-(Зх-4). Предложение не является предикатом; оно не является и высказыванием.
5) 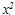 + +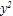 >0. Предложение является двухместным предикатом Q(x,y),Iq=R*R\{(0,0)}. >0. Предложение является двухместным предикатом Q(x,y),Iq=R*R\{(0,0)}.
Пример 2. Пусть даны предикаты А(х ,у) и В{х ,у), определенные на множестве 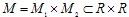 . Найти множество истинности предиката А(х, у) . Найти множество истинности предиката А(х, у)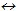 В{х,у) и изобразить ее с помощью кругов Эйлера-Венна. В{х,у) и изобразить ее с помощью кругов Эйлера-Венна.
Решение. Так как 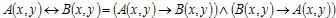 , то , то 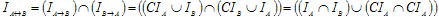 , , 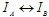 изображена заштрихованной частью рисунка. изображена заштрихованной частью рисунка.
 . .
Можно рассматривать и обратную задачу: Зная область истинности предиката, полученного в результате применения логических операций к некоторым предикатам, записать этот предикат.
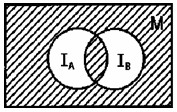
Пример 3. Записать предикат, полученный в результате логических операций над предикатами Р(x), Q(x) и R(x) , область истинности которого I заштрихована на рисунке.
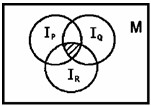 . .
Решение. Так как здесь 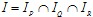 то искомый предикат имеет вид P(x)&Q(x)&R(x). то искомый предикат имеет вид P(x)&Q(x)&R(x).
Пусть имеется предикат Р(х), определенный на множестве М. Если а М, то подстановка а вместо х в предикат Р(х) превращает этот предикат в высказывание Р(a). Такое высказывание называется единичным. Наряду с образованием из предикатов единичных высказываний в логике предикатов рассматривается еще две операции, которые превращают одноместный предикат в высказывание. М, то подстановка а вместо х в предикат Р(х) превращает этот предикат в высказывание Р(a). Такое высказывание называется единичным. Наряду с образованием из предикатов единичных высказываний в логике предикатов рассматривается еще две операции, которые превращают одноместный предикат в высказывание.
Определение 3. Пусть Р(x)- предикат, определенный на множестве М. Под выражением 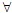 xP(x) понимают высказывание, истинное, когда Р(х) тождественно истинный на множестве М предикат и ложное в противном случае. xP(x) понимают высказывание, истинное, когда Р(х) тождественно истинный на множестве М предикат и ложное в противном случае.
Это высказывание уже не зависит от х. Соответствующее ему словесное выражение будет «Для всякого х Р(х) истинно». Символ 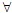 называют квантором всеобщности. Переменную х в предикате Р(х) называют свободной (ей можно придавать различные значения из М), в высказывании называют квантором всеобщности. Переменную х в предикате Р(х) называют свободной (ей можно придавать различные значения из М), в высказывании 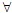 xP(x)переменную х называют связанной квантором xP(x)переменную х называют связанной квантором 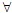 . .
Определение 4. Пусть Р(x) - предикат, определенный на множестве М. Под выражением 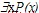 понимают высказывание, которое является истинным, если существует хотя бы один элемент х понимают высказывание, которое является истинным, если существует хотя бы один элемент х М, для которого Р(х) истинно, и ложным в противном случае. М, для которого Р(х) истинно, и ложным в противном случае.
Это высказывание уже не зависит от х. Соответствующее ему словесное выражение будет: «Существует х, при котором Р(х) истинно». Символ 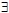 называют квантором существования. В высказывании называют квантором существования. В высказывании 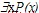 переменная х связана квантором переменная х связана квантором 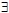 . .
Пример 4. Даны предикаты Р(х): 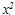 + x +1 >0 и Q{x): + x +1 >0 и Q{x): 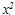 - 4х + 3 = 0, определенные на множестве R. Требуется установить, какие из следующих высказываний истинны и какие ложны: - 4х + 3 = 0, определенные на множестве R. Требуется установить, какие из следующих высказываний истинны и какие ложны:
1) 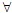 xP(x); 2) xP(x); 2) 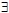 хР(х); 3) хР(х); 3) 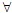 xQ(x); 4) xQ(x); 4) 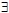 xQ(x). xQ(x).
Решение. Так как 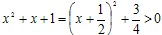 при всех x, то будут истинны высказывания при всех x, то будут истинны высказывания 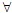 x Р(х) и x Р(х) и 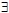 х Р(х). Так как уравнение х Р(х). Так как уравнение 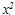 - 4х + 3 = 0 имеет только два действительных корня - 4х + 3 = 0 имеет только два действительных корня 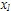 =3 и =3 и 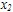 = 1, то предикат Q(x) принимает значение 1 только при х=3 и х=1 и 0 в остальных случаях. Но тогда высказывание = 1, то предикат Q(x) принимает значение 1 только при х=3 и х=1 и 0 в остальных случаях. Но тогда высказывание 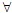 x Q(x) ложно, а высказывание x Q(x) ложно, а высказывание 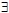 х Q(x) истино. х Q(x) истино.
Задание1: На множестве М = {1,2,3,...,20} заданы предикаты:
А(х): «х не делится на 5»;
B(x): «х- четное число»;
С(х): «х - число простое»;
D(x): «х кратно 3».
Найдите множества истинности следующих предикатов:
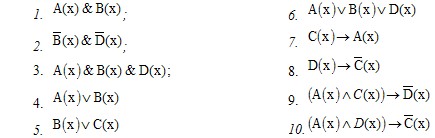
Задание 2: Записать предикаты, полученные в результате логических операций над предикатами Р(х), Q(x) и R(x) , области истинности которых заштрихованы на следующих рисунках:
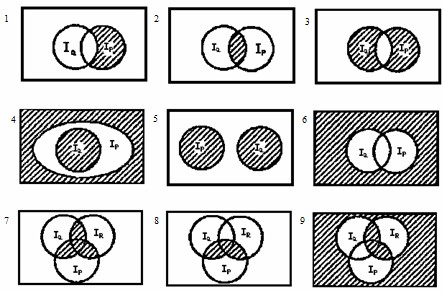
Задание3: Изобразить на диаграммах Эйлера- Венна области истинности следующих предикатов:

Задание 4: Установить, какие из следующих высказываний истинны, а какие ложны, при условии, что область определения предикатов М совпадает с R:
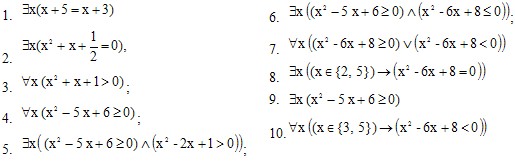
|
