Логические операции над высказываниями.
1. Отрицание. Отрицанием высказывания х называется новое высказывание 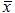 , которое истинно тогда и только тогда, когда х ложно, и ложно, если высказывание х истинно. , которое истинно тогда и только тогда, когда х ложно, и ложно, если высказывание х истинно.
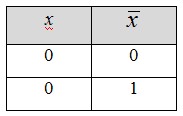
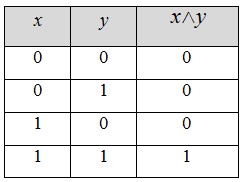
2. Конъюнкция (логическое умножение). Конъюнкцией двух высказываний х и у называется новое высказывание x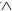 y , которое считается истинным, если оба высказывания х и у истинны, и ложным во всех остальных случаях. y , которое считается истинным, если оба высказывания х и у истинны, и ложным во всех остальных случаях.
Таблица истинности операции конъюнкции имеет следующий вид:
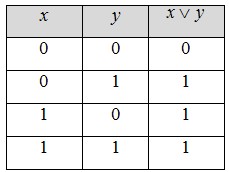
3. Дизъюнкция (логическое сложение). Дизъюнкцией двух высказываний х и у называется новое высказывание , которое считается ложным, если оба высказывания х и у ложны, и истинным во всех остальных случаях.
Эту операцию наглядно можно изобразить с помощью таблицы истинности:
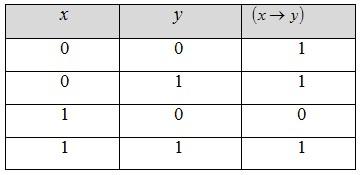
4. Импликация. Импликацией двух высказываний х и у называет новое высказывание (x y), которое считается ложным, если х- истинно, а у- ложно, и истинным во всех остальных случаях. y), которое считается ложным, если х- истинно, а у- ложно, и истинным во всех остальных случаях.
Высказывание х называют посылкой, а у – заключением.
Таблица истинности имеет следующий вид:
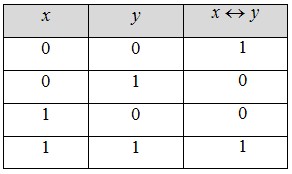
5. Эквиваленция. Эквиваленцией двух высказываний х и у называют новое высказывание x y , которое считается истинным, когда оба высказывания х и у либо одновременно истинны, либо одновременно ложны. y , которое считается истинным, когда оба высказывания х и у либо одновременно истинны, либо одновременно ложны.
Эту операцию наглядно можно изобразить с помощью таблицы истинности.
Символы 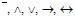 называются позиционными связками. Логическим связкам приписывают ранги в следующем порядке убывания старшинства: называются позиционными связками. Логическим связкам приписывают ранги в следующем порядке убывания старшинства: 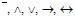 . Таким образом, связка более высокого ранга имеет большую область действия. . Таким образом, связка более высокого ранга имеет большую область действия.
Существуют операции, с помощью которых может быть выражена любая из пяти логических операций, рассмотренных выше. Такими операциями являются:
1. Штрих Шеффера (читается «А несовместно с В»). Эта операция обозначается x|y и определяется следующей таблицей истинности.
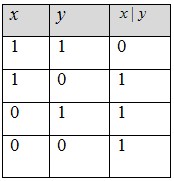
Имеет место следующее равенство x|y= 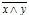
2. Стрелка Пирса(читается «ни А, ни В»). Эта операция обозначается x y и определяется следующей таблицей истинности. y и определяется следующей таблицей истинности.
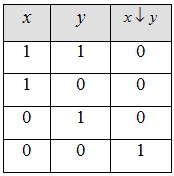
Имеет место следующее равенство x|y=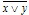
3. Сложение по модулю два (исключающее или). Эта операция обозначается x 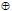 y и определяется следующей таблицей истинности. y и определяется следующей таблицей истинности.
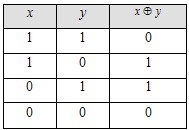
Имеет место следующее равенство x 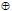 y= y=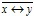
1. Составить таблицы истинности для формул:
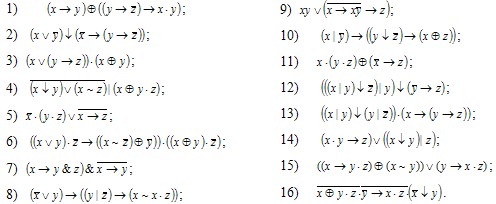
2. Выяснить, являются ли формулы тождественно истинными, тождественно ложными или выполнимыми:
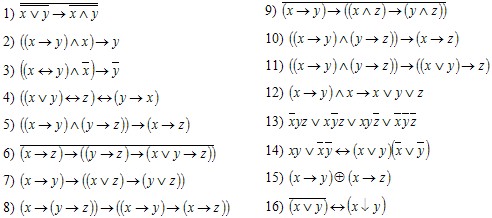
|
