Полнота и замкнутость системы функций Теорема Поста о полноте.
Для того чтобы система функций была полной, необходимо и достаточно, чтобы она не содержалась целиком ни в одном из классов T0, T1, L, S, M.
Пример7: Составим критериальную таблицу для системы функций:
{0, 1, x1x2, x1 x2}. x2}.
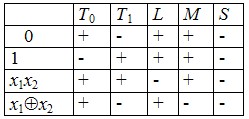
Согласно теореме Поста эта система полна.
Пример8: Выясним, полна ли система A=(LI T1)Y(S\T0) . Составим критериальную таблицу, очевидно LI T1 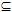 L,T1 . Чтобы показать, что LI T1 L,T1 . Чтобы показать, что LI T1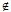 T0 , достаточно найти одну функцию f T0 , достаточно найти одну функцию f LI T1 и f LI T1 и f 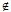 T0 . Возьмем T0 . Возьмем 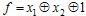 , удовлетворяющую требуемым условиям. Если f , удовлетворяющую требуемым условиям. Если f  S\T0, то f(0, ..., 0) = 1, f(1, ..., 1)=0, следовательно, f S\T0, то f(0, ..., 0) = 1, f(1, ..., 1)=0, следовательно, f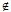 M, f M, f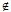 T1. Рассмотрим функцию h = T1. Рассмотрим функцию h = 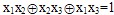 , набор ее значений (11101000), h , набор ее значений (11101000), h S\T0, но h S\T0, но h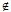 L. Следовательно, критериальная таблица имеет вид: L. Следовательно, критериальная таблица имеет вид:
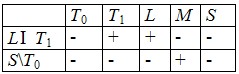
и А – полная система функций.
Задание 12. Выяснить, полна ли система функций:
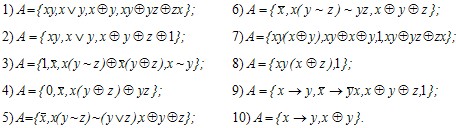
Задание 14. Выяснить, полна ли система А функций, заданных векторами своих значений:

Задание 15 . Выяснить, полна ли система А:
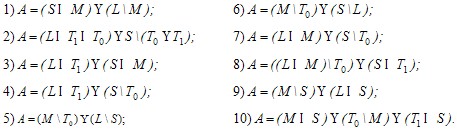
|
