Полином Жегалкина. Линейность и класс линейных функций.
Общий вид полинома Жегалкина:
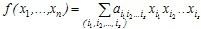
где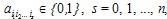 причем при s = 0 получаем свободный член а0. причем при s = 0 получаем свободный член а0.
Методы представления функции полиномом Жегалкина
1. Представим любую функцию формулой над 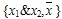 и сделаем замену и сделаем замену 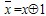 . Этот способ удобен, если функция задана формулой. . Этот способ удобен, если функция задана формулой.
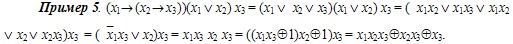
Надо помнить, что четное число одинаковых слагаемых в сумме по mod2 дает 0.
2. Метод неопределенных коэффициентов. Он удобен, если функция задана таблицей.
Пример 6. Запишем с неопределенными коэффициентами полином Жегалкина для функции трех переменных
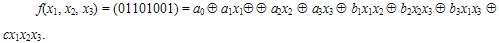
Затем находим коэффициенты, используя значения функции на всех наборах.
На наборе (0, 0, 0) f(0, 0, 0) = 0, с другой стороны, подставив этот набор в полином, получим f(0, 0, 0) = а0, отсюда а0 = 0. f(0, 0, 1) = 1, подставив набор (0, 0, 1) в полином, получим: f(0, 0, 1) = а0 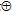 а3, т.к. а0 = 0, отсюда а3 = 1. Аналогично, f(0, 1, 0) = 1 а3, т.к. а0 = 0, отсюда а3 = 1. Аналогично, f(0, 1, 0) = 1
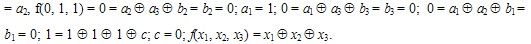
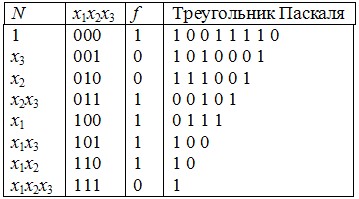
3. Многочлен Жегалкина можно получить также с помощью треугольника Паскаля по единицам его левой стороны по таблице следующим образом. Построим многочлен Жегалкина для функции f = (10011110). Верхняя сторона треугольника есть функция f. Любой другой элемент треугольника есть сумма по модулю для двух соседних элементов предыдущей строки. Левая сторона треугольника для функции f содержит шесть единиц. Многочлен Жегалкина будет содержать шесть слагаемых. Первая единица треугольника соответствует набору (000). Первое слагаемое многочлена есть 1. Третья снизу единица в левой стороне треугольника соответствует набору (101). В качестве слагаемого многочлена берем x1x3. Аналогично для других единиц треугольника. Слева от наборов показаны слагаемые многочлена Жегалкина.
Определение. Функция f(x1, ..., xn), полином Жегалкина для которой имеет следующий линейный относительно переменных вид: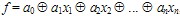 , называется линейной. Класс линейных функций обозначается L. , называется линейной. Класс линейных функций обозначается L.
Задание 5 . Методом неопределенных коэффициентов найти полиномы Жегалкина для следующих функций:
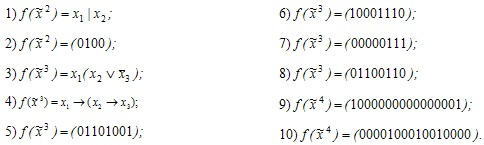
Задание 6. Методом треугольника Паскаля построить полином Жегалкина:
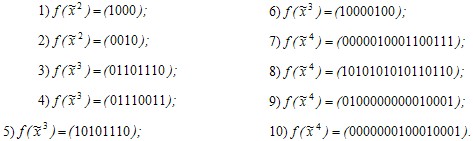
Задание 7 . Представив функцию f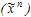 формулой над множеством связок формулой над множеством связок 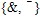 , преобразуйте её в полином Жегалкина , преобразуйте её в полином Жегалкина
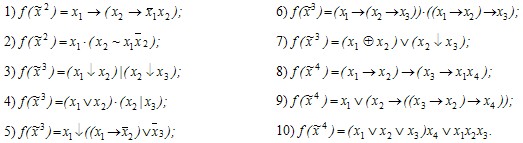
Задание 8. Представив функцию f полиномом, выяснить, является ли она линейной:
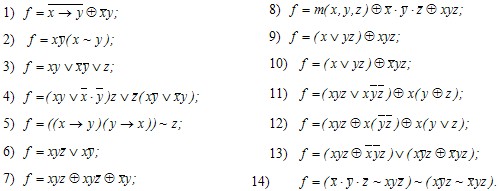
Задание 9. Выяснить, является ли линейной функция f, заданная векторно:
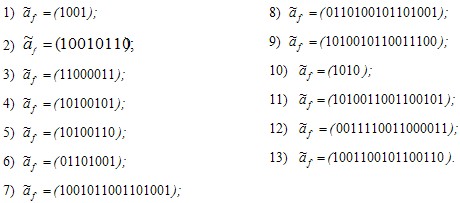
|
