Двойственность. Класс самодвойственных функций.
Определение. Функции f*(x1, ..., xn) называется двойственной к функции f(x1, ..., xn), если f*(x1, ..., xn) = 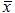 . .
Пример 1. Покажем с помощью таблицы истинности, что константа 0 двойственна к 1:
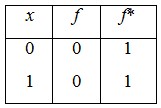
Функции f(x) = x и g(x) = 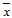 двойственны сами себе: двойственны сами себе:
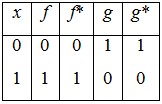
так как f*(0)= 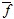 (1). (1).
Определение 2. Если f*(x1, ..., xn) = f(x1, ..., xn), то f(x1, ..., xn) называется самодвойственной.
Множество всех самодвойственных функций обозначается через S.
Пример 2. Покажем, что 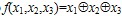 – самодвойственна. – самодвойственна.
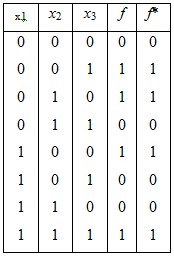
Если f*– самодвойственна, то 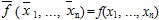 , т.е. на противоположных наборах функция принимает противоположные значения. , т.е. на противоположных наборах функция принимает противоположные значения.
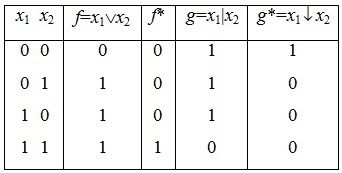
Пример 3. Покажем, что функция х1 v х2 двойственна к x1&x2, функция х1  х2 двойственна к функции x1|x2. х2 двойственна к функции x1|x2.
Пример 4. Построить формулу, реализующую f*, если f = ((x  y) v z) (y y) v z) (y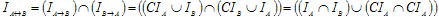 (x (x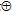 yz)). Покажем, что она эквивалентна формуле N = z(x yz)). Покажем, что она эквивалентна формуле N = z(x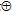 y). y).
Найдем (x y)* и (x y)* и (x y)*. y)*.
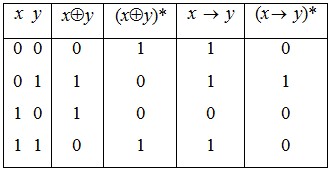
Из таблиц видно, что
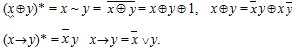
По принципу двойственности:
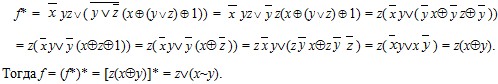
Задание 1 . Используя непосредственно определение двойственности булевых функций, выясните, является ли функция g двойственной к функции f:

Задание 2 . Используя принцип двойственности, постройте формулу, реализующую функцию, двойственную к функции f, и убедитесь в том, что полученная формула эквивалентна формуле V:
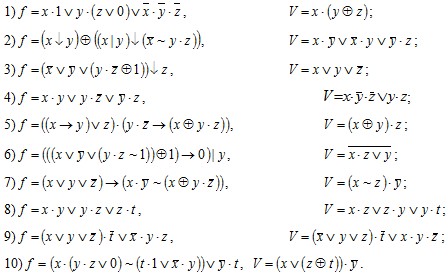
Задание 3 . Выяснить, является ли функция f самодвойственной:

Задание 4 . Представив функцию f полиномом, выяснить, является ли она линейной:
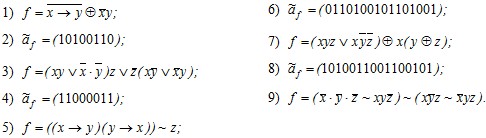
|
