|

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ЦЕНТР ДИСТАНЦИОННОГО ОБУЧЕНИЯ
Кафедра «Сервис и техническая эксплуатация автотранспортных средств»
Конструкция, расчет и потребительские свойства автомобилей
ЭКСПЛУАТАЦИОННЫЕ СВОЙСТВА АВТОМОБИЛЯ
ТЕОРИЯ И РАСЧЕТ
Учебное пособие
2.3. Поворот автомобиля с эластичными колесами и условия сохранения управляемости
При качении эластичного колеса автомобиля, нагруженного боковой силой, отпечаток на дорожном покрытии повернется
относительно плоскости колеса, и оно будет двигаться не в плоскости своей симметрии, а под углом δ к ней (рис. 9).
Угол поворота δ называют углом увода колеса.
При движении автомобиля боковая сила может быть центробежной при повороте, может быть ветровой нагрузкой
или составляющей силы веса автомобиля при его движении по дороге, имеющей поперечный уклон.
Результаты большого числа экспериментов, проведенных в различных странах различными исследователями, показали,
что зависимость между углами увода и боковыми силами в общем случае нелинейна. При малых углах увода изменение
отношения Рб/δ сравнительно невелико и может считаться постоянным (Рб/δ=Ку=const), а зависимость Рб=f(δ), следовательно, линейной.
Отношение Рб/δ получило название коэффициента сопротивления уводу.
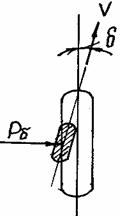
Рис. 9. Схема колеса, нагруженного боковой силой
Коэффициент сопротивления уводу Ку зависит от большого числа факторов, основными из них являются:
размеры и конструкция колеса; давление воздуха в шине; величина сил, действующих на колесо; скорость движения;
тип и состояние дорожного покрытия; форма траектории движения центра колеса (прямолинейная, криволинейная, кривизна траектории и скорость
ее изменения по времени или пути); характер приложения сил, действующих на колесо, и скорость изменения этих сил.
Для шин легковых автомобилей отечественных марок «Москвич» и ГАЗ «Волга» коэффициент сопротивления уводу Ку
имеет значения соответственно 360 и 470 Н/град.
При движении автомобиля с жесткими колесами центр его поворота определяется точкой О (рис. 10) пересечения прямых,
являющихся продолжениями осей колес, а расстояние от этой точки до продольной плоскости симметрии автомобиля определяет радиус поворота R.
| Этот радиус поворота равен |
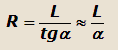 |
где α– средний угол поворота управляемых колес.
При повороте автомобиля с эластичными колесами под действием центробежной силы возникает увод каждого колеса,
что приводит к смещению центра поворота. Центр поворота О' в этом случае будет лежать на пересечении перпендикуляров,
восстановленных из середины переднего и заднего мостов к направлениям их движения. Направление движения задней оси будет отклоняться от
средней плоскости автомобиля на угол увода δВ, а направление движения передней оси – на угол увода δА.
Радиус поворота R' автомобиля в этом случае можно определить из схемы на рис. 10:
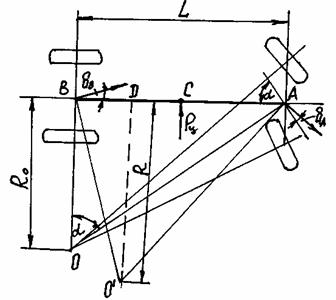
Рис. 10. Схема поворота автомобиля с эластичными колесами
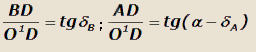
L=AD+BD=O1D·tg(α-δA)+O1D·tgδB
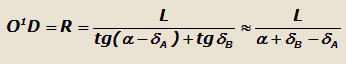 |
(16) |
Из уравнения (16) следует, что величина действительного радиуса поворота R зависит не только от среднего угла α поворота
управляемых колес, а также и от соотношения между углами увода передней δA и задней δВ осей.
Из уравнения (16) видно, что может быть три случая движения автомобиля:
| 1. Углы увода передней и задней осей равны (δA=δB). В этом случае радиус поворота определяется выражением: |
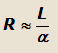 |
т.е. он будет приблизительно равен радиусу поворота автомобиля с жесткими колесами;
| 2. Угол увода передней оси больше угла увода задней оси ( δA > δB ). В этом случае: |
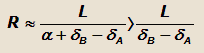 |
т.е. радиус поворота автомобиля с эластичными колесами больше радиуса поворота автомобиля с жесткими колесами;
3. Угол увода передней оси меньше угла увода задней оси ( δA < δB ). В этом случае: |
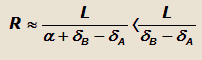 |
т.е. радиус поворота автомобиля с эластичными колесами будет меньше радиуса поворота автомобиля с жесткими колесами.
В соответствии с этим автомобиль, имеющий угол увода передней оси больше, чем задней, называют обладающим свойством
недостаточной поворачиваемости, а автомобиль, у которого угол увода передней оси меньше чем задней – обладающим свойством излишней
поворачиваемости.
Автомобили, обладающие излишней и недостаточной поворачиваемостью, по-разному ведут себя при прямолинейном движении.
Если к автомобилю с излишней поворачиваемостью и движущемуся прямолинейно приложить боковую силу Рб, то из-за бокового
увода колес траектория его движения изменится. Автомобиль начнет двигаться по окружности с центром, расположенным в точке О (рис. 10).
Центробежная сила инерции Рц, как видно из рис. 10, будет направлена в ту же сторону, что и боковая сила Рб. Это еще увеличит углы увода, уменьшит
радиус поворота, а следовательно, увеличит центробежную силу, что снова приведет к увеличению углов увода и т.д. Если при этом водитель не изменит положения
управляемых колес для увеличения радиуса поворота, то может начаться занос задней оси автомобиля.
Составляя схему действия боковой и центробежной сил на автомобиль с недостаточной поворачиваемостью и движущийся
прямолинейно, можно показать, что центробежная сила Рц будет направлена противоположно действующей силе Рб. Это приведет к
уменьшению углов увода и выравниванию направления движения автомобиля.
Из формулы (16) следует, что при движении автомобиля с неповернутыми управляемыми колесами (угол a=0) возможен такой
случай, когда произойдет поворот автомобиля и начнется его движение по траектории с радиусом
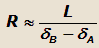
Физический смысл явления может быть объяснен тем, что при кратковременном действии боковой силы из-за увода колес,
автомобиль начинает двигаться по кривой. Возникающая центробежная сила Рцувеличивает этот увод и в дальнейшем даже
при прекращении действия кратковременной силы, вызывает движение по кривой все уменьшающегося радиуса.
Боковая сила может возникнуть из-за порыва ветра, наклона дороги и т.д., а скорость, при которой начнется движение
автомобиля по кривой, получила название критической.
Величина центробежной силы, которая действует на повороте при движении автомобиля с критической скоростью,
будет равна:
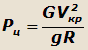
Подставляя в это выражение значение радиуса поворота, получим:
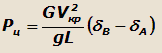
Отсюда критическая скорость движения будет равна:
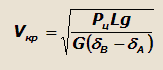
Углы увода δB и δA могут быть выражены:
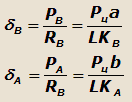
где PA и PB – составляющие центробежной силы, приходящейся на переднюю и заднюю оси автомобиля;
a и b – продольные координаты центра масс автомобиля.
Подставляя эти значения δA и δB в выражение для критической скорости, получим:
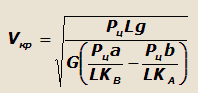
или окончательно
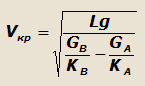 |
(17) |
где GA и GB – составляющие силы веса автомобиля, приходящиеся на переднюю и заднюю оси.
Анализ выражения (17) позволяет установить, что увеличение продольной базы автомобиля увеличивает его критическую
скорость и критическая скорость изменяется в зависимости от распределения силы веса автомобиля по осям и соотношения
коэффициентов сопротивления уводу передней и задней осей.
Из выражения (17) следует также, что при анализе критической скорости возможны три случая:
| 1) |
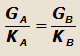 |
Vкр = ∞, т.е. в этом случае критическая скорость весьма велика. |
| 2) |
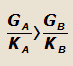 |
подсчет по формуле (17) приведет к получению мнимых величин, т.е. критическая скорость невозможна вообще |
(автомобиль с недостаточной поворачиваемостью).
| 3) |
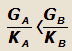 |
критическая скорость может иметь расчетное значение, при котором достаточно появление сколь угодно |
малой силы, чтобы автомобиль потерял управляемость (автомобиль с излишней поворачиваемостью).
Таким образом, для получения хорошей управляемости, автомобиль должен иметь параметры, обеспечивающие выполнение
первого или второго условия.
Уравнения для определения (δB – δA), Рц и R связывают пять различных переменных величин R, a, V, Pц и (δB – δA).
Если две из этих величин заданы, то остальные три будут иметь строго определенные значения. Например, если автомобиль движется по кругу
заданного радиуса R с определенной скоростью V, то управляемые колеса должны быть повернуты на определенный угол ?, центробежная сила Рц и углы увода δA и δB
будут иметь также вполне определенные значения.
Для количественного анализа параметров, от которых зависит управляемость автомобиля, строят график управляемости,
используя при этом уравнение (16). Рассмотрим порядок построения графики управляемости для автомобиля с излишней поворачиваемостью.
Отложим по оси абсцисс (рис. 11) разность δB–δA.
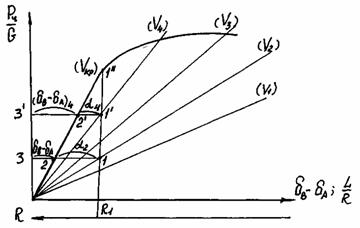
Рис. 11. График управляемости автомобиля
По оси ординат отложим удельную центробежную силу Рц/G. Зависимость между отношением Рц/G и разностью δB–δA будет
аналогична зависимости между боковой силой и углом увода отдельного колеса. Для оценки влияния радиуса поворота отложим по горизонтальной оси также величину L/R.
Из уравнения (16): L/R = α + δB – δA , т.е. для того, чтобы отложить величину L/R по оси абсцисс можно воспользоваться той же шкалой, что и для величины δB – δA.
Для удобства пользования графиком под шкалой δB – δA и L/R нанесем еще шкалу значений R.
Для постоянной скорости движения автомобиля график функции Рц/G = f(L/R) выразится прямой, проходящей через начало
координат, так как:
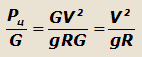
| или |
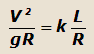 |
| откуда |
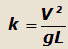 |
где k – угловой коэффициент.
Построив для нескольких постоянных скоростей, в том числе для расчетной критической скорости, эти зависимости, получим
пучок прямых,проходящих через начало координат. Теперь каждый случай движения автомобиля можно характеризовать одной точкой на
графике. Пусть, например, автомобиль движется по кривой с радиусом R1 и скоростью V2. Такой случай движения будет характеризоваться на графике точкой 1.
Проведя горизонтальную прямую через эту точку, получим точку 2 ее пересечения с графиком для критической скорости и точку 3 пересечения с осью ординат.
Отрезок 1-2 определит величину угла α2 поворота управляемых колес, отрезок 2-3 – величину разности (δB–δA)2.
Из рис. 11 следует, что если при движении по дуге того же радиуса увеличить скорость автомобиля до V4, то данный случай
будет характеризоваться уже точкой 1', разность углов увода (δB – δA) 4 колес тоже увеличится и будет равной отрезку 2'–3', а угол
поворота ?4 управляемых колес уменьшиться и определится длиной отрезка 1'–2'. При дальнейшем увеличении скорости угол поворота управляемых колес будет
уменьшаться и при критической скорости (точка 1'') будет равен нулю. Автомобиль будет двигаться по кругу с неповернутыми колесами и кривизна траектории
его движения будет определяться только величиной разности углов увода δB–δA.
Кроме рассмотренных выше конструктивных и кинематических параметров при анализе управляемости автомобиля необходимо
учитывать влияние на управляемость конструкции подвески и форму кузова автомобиля.
Влияние конструкции подвески на управляемость автомобиля объясняется зависимостью угла увода колес от их наклона к
плоскости дороги. При повороте автомобиля колеса с независимыми (рычажными) подвесками наклоняются в сторону, противоположную
от центра поворота и возникающие при этом дополнительные уводы колес увеличивают уводы от действия центробежных сил инерции. Чтобы не создавать для
автомобиля условий избыточной поворачиваемости и тем самым повысить его управляемость, задние колеса автомобилей, как правило, устанавливают на зависимых подвесках.
Форма кузова легкового автомобиля оказывает существенное влияние на управляемость потому, что она определяет точку
метацентр) приложения равнодействующей сил, вызванных боковым ветром. Рассмотрим схему сил, действующих на прямолинейно
движущийся автомобиль при наличии бокового ветра (рис. 12). Боковая сила Pб, вызванная ветром, приложена в метацентре кузова. У одних автомобилей
эта точка расположена перед центром масс, у других – за ним.
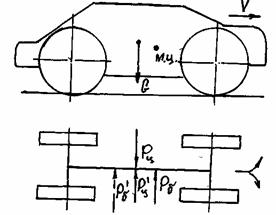
Рис. 12. Схема сил, действующих на автомобиль при боковом ветре.
Действие бокового ветра вызывает увод передней и задней осей автомобиля. Если метацентр расположен впереди центра масс,
то автомобиль начнет поворачиваться в направлении действия ветра. Это вызовет появление центробежной силы Pц, которая
образуя с силой ветра Рб момент, увеличит стремление автомобиля к повороту. Если метацентр расположен за центром масс автомобиля, то при
действии бокового ветра (боковая сила Рб'), автомобиль будет стремиться повернуться против ветра. Возникшая при этом центробежная сила Рц'
будет стремиться уменьшить поворот автомобиля. Поэтому для обеспечения автомобилю наилучшей управляемости при боковом ветре, необходимо кузову
придавать такую форму, чтобы метацентр был расположен за центром масс. Для смещения метацентра назад понижают капот двигателя, а в задней части
применяют высокое оперение задних крыльев.
|
