Наименование работы: моделирование динамики популяций
Цель работы: построение и анализ моделей развития популяций в различных условиях их существования
Содержание работы:
1 Модель динамики популяции Мальтуса
Исследование динамики популяции провести при следующих допущениях:
- факторы экологической ниши, сдерживающие рост популяции, отсутствуют,
- скорость прироста численности популяции прямо пропорциональна величине численности популяции
Пусть x(t) – численность популяции в момент времени t. Функцией прироста R(t) называется относительное изменение численности популяции за время Δt:
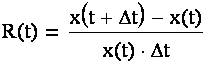
Если эта величина постоянна: R(t) = r, то закон, управляющий динамикой в модели Мальтуса, имеет вид:
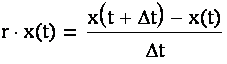
Переходя к пределу по Δt, получим следующее обыкновенное дифференциальное уравнение:
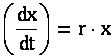
Для решения поставленной задачи небходимо найти решение данного уравнения при начальном условии x(0) = x0. Воспользуемся методом разделения переменных:
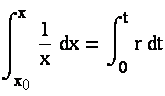
и окончательно получим: x = x0ert
Для визуализации результатов построить графики зависимости при различных x0, t и r. Сделать выводы о характере роста популяции согласно модели Мальтуса.
Ниже приведен рабочий документ для построения графиков в пакете Mathcad.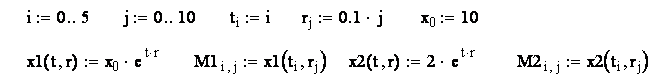
2 Модель динамики популяции Ферхюльста
Исследование динамики популяции провести при следующих допущениях:
- любая экологическая ниша может обеспечить существование популяции только определенного максимального размера xmax,
- скорость прироста численности популяции должна снижаться, когда размеры популяции приближаются к xmax.
Если измерять численность популяции в относительных единицах:
X = x/ xmax, то функция прироста по Фюнхельсту будет равна:
R(X) = r(1 – X)
Тогда математическую модель динамики популяции по Ферхюльсту можно представить ввиде следующего ОДУ:
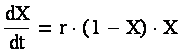
при следующих начальных условиях: X(0) = X0
Проинтегрировав уравнение методом разделения переменных:
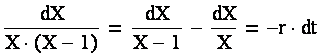
получим решение:
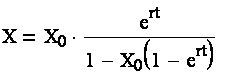
Для визуализации результатов построить графики зависимости при различных X0, t и r аналогично п.1. Сделать выводы о характере роста популяции согласно модели Ферхюльста.
3 Модель соперничества двух популяций (модель Брауна-Гордона)
Исследование модели провести при следующих допущениях:
- в экологической нише сосуществуют две популяции, взаимодействующие друг с другом: хищники и добыча,
- запасы пищи для добычи в отсутствие хищников не ограничиваются,
- добыча является единственным источником пищи для хищников.
Пусть x(t) и y(t) – текущая численность особей добычи и хищников соответственно. В отсутствие хищников темп прироста добычи составит rx(t). Сосуществование с хищниками повысит уровень смертности добычи пропорционально произведению численности обеих популяций: x(t)y(t). Поэтому общий темп изменения популяции добычи может быть представлен как:
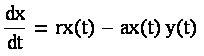
где а – положительный коэффициент пропорциональности.
Поскольку существование самих хищников зависит от популяции добычи, темп изменения популяции хищников в отсутствие добычи составляет –sy(t), где s – прирост хищников при неограниченном количестве добычи.
Взаимодействие между популяциями приводит к росту популяции хищников пропорционально x(t)y(t). Следовательно общий темп изменения популяции хищников составляет:
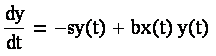
где b - положительный коэффициент пропорциональности.
Математическая модель соперничества двух популяций будет выглядеть следующим образом:
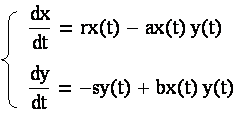
Получить численное решение модели в пакете Mathcad с использованием метода Рунге-Кутта при следующих условиях:
x(0) = 12000, y(0) = 600, r = 0.001, s = 0.01, a = 2x10-6, b = 10-6
Порядок решения системы ОДУ в пакете Mathcad:
- определить вектор, содержащий начальные значения для каждой функции
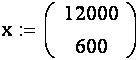
- определить функцию, возвращающую значение ввиде вектора из двух элементов, содержащих первые производные каждой из функций,
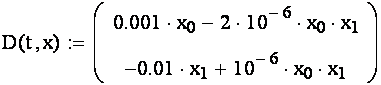
- выбрать точки, в которых необходимо найти решение системы и передать всю информацию в функцию rkfixed
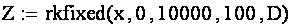
Функция rkfixed возвращает матрицу, чей первый столбец содержит точки, в которых ищется приближенное решение, остальные столбцы содержат значения найденных приближенных решений в соответствующих точках.
Для визуализации результатов построить графики численного решения при различных начальных условиях, а также значениях r, s, a и b. Сделать выводы о характере соперничества двух популяций согласно модели Брауна-Гордона.
4. Добавить в модель Брауна-Гордона случайную компоненту и проанализировать условия сосуществования двух популяций при наличии случайных воздействий различной интенсивности.